Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 37

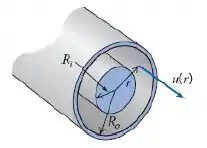
O perfil de velocidade para escoamento laminar em uma seção anular é dado por

u r = - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r    

em que Δ p / L = - 10   k P a / m é o gradiente de pressão, μ é a viscosidade (óleo SAE 10 a 20 ℃ ) e R 0 = 5   m m e R i = 1   m m são os raios externo e interno do anel. Determine a vazão volumétrica, a velocidade média e a velocidade máxima. Faça um gráfico da distribuição de velocidades.

Passo 1

Nos foi dado no enunciado que:

O perfil de velocidade em um espaço anular é:

u r = - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r    

Δ p / L = - 10   k P a / m

Raio externo: R 0 = 5   m m = 0,005   m .

Raio interno: R i = 1   m m = 0,001   m .

A viscosidade é do óleo SAE 10 que flui através do anel a 20 ℃ : μ = 0,1   P a ⋅ s .

Passo 2

Consideramos que o escoamento esteja em estado estacionário, escoamento unidirecional e que o fluido seja incompressível, podemos escrever a vazão do volume através da seção anular como:

Q ˙ = ∫ V → ⋅ d A →

Assim, para qualquer seção a vazão pode ser escrita como:

Q ˙ = ∫ u   d A

Onde, nós podemos escrever d A como:

d A = 2 π r d r

Passo 3

Para encontrarmos a vazão volumétrica, basta substituirmos os valores dados no enunciado na integral, e integrarmos de R i a R 0 . Assim temos:

Q ˙ = ∫ R i R 0 u   d A

Q ˙ = 2 π ∫ R i R 0 u r d r

Q ˙ = 2 π ∫ R i R 0 - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r     r d r

Q ˙ = - π ∆ p 2 μ L ∫ R i R 0 r R 0 2 - r 3 + R 0 2 - R i 2 ln ⁡ R i R 0 r ln ⁡ R 0 r     d r

Q ˙ = - π ∆ p 2 μ L ∫ R i R 0 r R 0 2 d r - ∫ R i R 0 r 3 d r + R 0 2 - R i 2 ln ⁡ R i R 0 ∫ R i R 0 r ln ⁡ R 0 r d r    

Q ˙ = - π ∆ p 2 μ L r 2 2 R 0 2 R i R 0 - r 4 4 R i R 0 + R 0 2 - R i 2 ln ⁡ R i R 0 ∫ R i R 0 r ln ⁡ R 0 r d r    

Q ˙ = - π ∆ p 2 μ L R 0 4 2 - R i 2 R 0 2 2   - R 0 4 4 + R i 4 4 + R 0 2 - R i 2 ln ⁡ R i R 0 ∫ R i R 0 r ln ⁡ R 0 r d r    

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ∫ R i R 0 r ln ⁡ R 0 r d r    

Passo 4

Para resolver a integral

∫ R i R 0 r ln ⁡ R 0 r d r

Precisamos usar o método de integração por partes. Vamos então resolver separadamente e depois voltar com os valores encontrados.

∫ R i R 0 r ln ⁡ R 0 r d r = r 2 2 ln ⁡ R 0 r R i R 0 - ∫ R i R 0 r 2 2 1 R 0 / r - R 0 r 2 d r

∫ R i R 0 r ln ⁡ R 0 r d r = r 2 2 ln ⁡ R 0 r R i R 0 - ∫ R i R 0 - r 2 d r

∫ R i R 0 r ln ⁡ R 0 r d r = r 2 2 ln ⁡ R 0 r R i R 0 + r 2 4 R i R 0

∫ R i R 0 r ln ⁡ R 0 r d r = R 0 2 2 ln ⁡ R 0 R 0 - R i 2 2 ln ⁡ R 0 R i + R 0 2 4 - R i 2 4

∫ R i R 0 r ln ⁡ R 0 r d r = R 0 2 2 ln ⁡ 1 - R i 2 2 ln ⁡ R 0 R i + R 0 2 - R i 2 4

∫ R i R 0 r ln ⁡ R 0 r d r = - R i 2 2 ln ⁡ R 0 R i + R 0 2 - R i 2 4

Passo 5

Agora, podemos substituir o resultado da integral encontrada no passo 4 na equação

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ∫ R i R 0 r ln ⁡ R 0 r d r    

Assim pomos encontrar a vazão volumétrica.

Substituindo temos:

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R 0 2 - R i 2 ln ⁡ R i R 0 - R i 2 2 ln ⁡ R 0 R i + R 0 2 - R i 2 4    

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R 0 2 - R i 2 ln ⁡ R i - ln ⁡ R 0 - R i 2 2 ln ⁡ R 0 - ln ⁡ R i + R 0 2 - R i 2 4    

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R 0 2 - R i 2 ln ⁡ R i - ln ⁡ R 0 R i 2 2 - ln ⁡ R 0 + ln ⁡ R i + R 0 2 - R i 2 4    

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R i 2 R 0 2 - R i 2 ln ⁡ R i - ln ⁡ R 0 2 ln ⁡ R i - ln ⁡ R 0 + R 0 2 - R i 2 2 4 ln ⁡ R i - ln ⁡ R 0    

Q ˙ = - π ∆ p 2 μ L R 0 4 + R i 4 4 - R i 2 R 0 2 2 + R i 2 R 0 2 - R i 2 2 + R 0 2 - R i 2 2 4 ln ⁡ R i R 0    

Q ˙ = - π ∆ p 2 μ L R 0 4 4 + R i 4 4 - R i 2 R 0 2 2 + R i 2 R 0 2 2 - R i 4 2 + R 0 2 - R i 2 2 4 ln ⁡ R i R 0    

Q ˙ = - π ∆ p 2 μ L R 0 4 4 + R i 4 - 2 R i 4 4 + R i 2 R 0 2 - R i 2 R 0 2 2 + R 0 2 - R i 2 2 4 ln ⁡ R i R 0    

Q ˙ = - π ∆ p 2 μ L R 0 4 4 - R i 4 4 + R 0 2 - R i 2 2 4 ln ⁡ R i R 0    

Q ˙ = - π ∆ p 2 μ L R 0 4 - R i 4 4 + R 0 2 - R i 2 2 4 ln ⁡ R i R 0    

Passo 6

Podemos substituir na equação encontrado no passo 5, os valores fornecidos no enunciado. Assim temos:

Q ˙ = - π ∆ p 2 μ L R 0 4 - R i 4 4 + R 0 2 - R i 2 2 4 ln ⁡ R i R 0    

Q ˙ = - π - 10 × 10 3   P a / m 2 0,1   P a ⋅ s 0,005   m 4 - 0,001   m 4 4 + 0,005   m 2 - 0,001   m 2 2 4 ln ⁡ 5 1    

Q ˙ = 157079,63 m ⋅ s 6,65 × 10 - 11   m 4

Q ˙ = 1,044 × 10 - 5   m 3 / s

Portanto, a taxa de fluxo de volume é 1,044 × 10 - 5   m 3 / s .

Passo 7

Podemos encontrar a velocidade média com a seguinte formula:

V = Q ˙ A

V = Q ˙ π R 0 2 - R i 2

Substituindo os valores temos:

V = 1,044 × 10 - 5   m 3 / s π 0,005 2 - 0,001 2 m 2

V = 0,133   m / s

Assim, temos que a velocidade média é 0,133   m / s .

Passo 8

Precisamos saber que a velocidade máxima ocorre quando d u d r = 0 . Assim, precisamos primeiro derivar o perfil de velocidade e igualar a zero. Derivando temos:

d d r - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r     = 0

d d r R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r     = 0

d d r R 0 2     - d d r r 2 + d d r R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r     = 0

0 - 2 r + R 0 2 - R i 2 ln ⁡ R i R 0 × 1 R 0 / r × - R 0 r 2 = 0

- 2 r + R 0 2 - R i 2 ln ⁡ R i R 0 × - 1 r = 0

2 r = - R 0 2 - R i 2 ln ⁡ R i R 0 × 1 r

r 2 = - R 0 2 - R i 2 2 ln ⁡ R i R 0

r 2 = R 0 2 - R i 2 2 ln ⁡ R 0 R i

Podemos agora substituir os valore na equação apara encontrar r .

r 2 = 0,005 2 - 0,001 2 2 ln ⁡ 5 1

r = 2,73   m m

Portanto a velocidade máxima ocorre quando r = 2,73   m m .

Passo 9

Assim, podemos encontrar a velocidade máxima u m á x calculando u 2,73 . Substituindo temos:

u r = - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r    

u m á x = - - 10 × 10 3 4 0,1 0,005 2 - 0,002 73 2 + 0,005 2 - 0,001 2 ln ⁡ 1 5 ln ⁡ 5 2,73    

u m á x = 0,205   m / s

Portanto, a velocidade máxima é 0,205   m / s

Passo 10

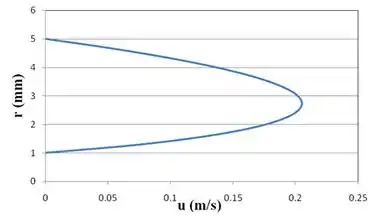
Usando a equação do perfil de velocidade fornecida, a distribuição de velocidade no anel é plotada usando o Excel.

Resposta

Q ˙ = 1,044 × 10 - 5   m 3 / s

V m é i d a = 0,133   m / s

u m á x = 0,205   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Gasoline enters section 1 in Fig. P3.18 at 0.5 m3/s. It leavessection 2 at an average velocity of 12 m/s. What is the average velocity at section 3? Is it in or out?
The hypodermic needle in Fig. P3.23 contains a liquidserum (SG 5 1.05). If the serum is to be injected steadilyat 6 cm3/s, how fast in in/s should the plunger be advanced(a) if leakage in the plunger
A thin layer of liquid, draining from an inclined plane, as inFig. P3.26, will have a laminar velocity profile u U0(2y/h 2 y2/h2), where U0 is the surface velocity. If theplane has width b into the pa
Water flows from a faucet into a sink at 3 U.S. gallonsper minute. The stopper is closed, and the sink has two rectangular overflow drains, each 3/8 in by 1¼ in. If the sinkwater level remains constan
For the two-port tank of Fig. E3.5, assume D1 5 4 cm,V1 5 18 m/s, D2 5 7 cm, and V2 5 8 m/s. If the tank surfaceis rising at 17 mm/s, estimate the tank diameter.