Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 43

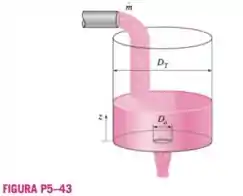
A água entra em um tanque com diâmetro D , de forma constante a uma vazão de massa de m e ˙ . Um orifício na parte inferior com diâmetro D 0 permite que a água escape. O orifício tem uma entrada arredondada, de modo que as perdas por atrito são desprezíveis. Se o tanque está inicialmente vazio, (a) determine a altura máxima que a água atingira no tanque e (b) obtenha uma relação para a altura da água z como função do tempo.

Passo 1

Aqui temos um problema diferente dos outros que já vimos, temos um orifício por onde a água escapa e ao mesmo tempo temos água entrando. Como as perdas por atrito são desprezíveis podemos usar a equação de Bernoulli.

Mas para começar facilitando a nossa vida, vamos começar “diagramando” estabelecendo nossos pontos 1 e 2 :

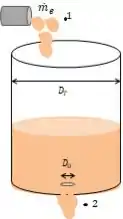
Passo 2

Pelo diagrama, os pontos 1 e 2 são expostos a atmosfera, ou seja, P 1 = P 2 = P a t m . Além disso, o nosso ponto de referência é em z 2 = 0 e a velocidade no ponto 1 é praticamente desprezível, ou seja, V 1 ≅ 0 . Assim, temos:

P 1 ρ g + V 1 2 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2

z 1 = V 2 2 2 g

V 2 = 2 g z 1

Como temos uma vazão mássica entrando podemos usá-la para encontrar a altura máxima:

m ˙ = ρ v ˙

Substituindo,

m e ˙ = ρ π D 0 2 4 2 g z 1

Assim, podemos isolar a altura z 1 referente a altura do tanque:

4 m e ˙ ρ π D 0 2 2 = 2 g z 1

z 1 = 1 2 g 4 m e ˙ ρ π D 0 2 2

Passo 3

Para colocarmos essa altura em função de um tempo, vamos lembrar que há dois momentos: uma entrada e uma saída.

A nossa ideia é colocar a vazão mássica em função do tempo:

d m ˙ s = ρ v ˙ d t                   ∴                   d m ˙ s = ρ π D 0 2 4 2 g z 1 d t

d m ˙ T = ρ A d z                     ∴                   d m ˙ T = ρ π D T 2 4 d z

Agora vamos organizar, no tanque temos uma vazão que entra menos a que sai, ou seja, a massa é conservada:

d m ˙ T = m e ˙ - ρ π D 0 2 4 2 g z 1 d t

ρ π D T 2 4 d z = m e ˙ - ρ π D 0 2 4 2 g z 1 d t

Organizando, obtemos uma expressão em função da altura e do tempo:

ρ π D T 2 4 d z m e ˙ - ρ π D 0 2 4 2 g z 1 = d t

Como essa integral é impossível de fazermos a mão, podemos utilizar um software como EES, o qual nos dará a seguinte resposta:

t = ρ π D T 2 2 ρ π D 0 2 4 2 g 2 ρ π D 0 2 4 2 g z 1 - m e ˙ ln ⁡ m e ˙ - ρ π D 0 2 4 2 g z 1 m e ˙

Prontinho!!

Resposta

(a) z 1 = 1 2 g 4 m e ˙ ρ π D 0 2 2

(b) t = ρ π D T 2 2 ρ π D 0 2 4 2 g 2 ρ π D 0 2 4 2 g z 1 - m e ˙ ln ⁡ m e ˙ - ρ π D 0 2 4 2 g z 1 m e ˙

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Descreva a distribuição de pressões sobre o exterior de um edifício de lojas sujeito a um vento em regime permanente. Identifique os locais de pressões máxima e mínima sobre o lado externo do prédio.
Um aspirador produz sucção por meio de uma corrente de água escoando através de um venturi. Analise a forma e as dimensões de tal aparelho. Comente sobre as limitações sobre o seu uso.
Imagine uma mangueira de jardim com um jato de água saindo através de um bocal na ponta da mangueira. Explique por que a extremidade da mangueira pode ficar instável, quando ela é segura a cerca de me
Considere o sistema de escoamento constituído de reservatório e discos, com o nível do reservatório constante, conforme mostrado. O escoamento entre os discos é iniciado do repouso em t = 0 . Avalie a
Aplique a equação de Bernoulli para escoamento não permanente ao manômetro de tubo em U de diâmetro constante mostrado. Considere que o líquido no manômetro é inicialmente deslocado pela aplicação de