Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 88
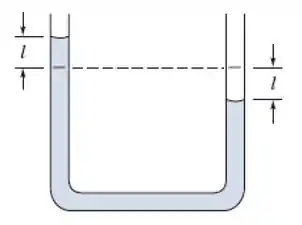
Aplique a equação de Bernoulli para escoamento não permanente ao manômetro de tubo em U de diâmetro constante mostrado. Considere que o líquido no manômetro é inicialmente deslocado pela aplicação de um diferencial de pressão e, em seguida, liberado. Obtenha uma equação diferencial para como uma função do tempo.
Passo 1
Tá legal, vamos começar o exercício aplicando a equação de Bernoulli para regime transiente entre os pontos 1 e 2 do manômetro:
Nesse caso, como os pontos 1 e 2 estão expostos à atmosfera, temos e os termos de pressão se cancelam. Nesse caso, devido a simetria do problema, da ausência de forças externas e da seção do manômetro ser constante, temos então que e os termos de velocidade também se cancelam, então a equação se torna:
Passo 2
Sabemos que a velocidade é o taxa de mudança da distância em função do tempo, só que no nosso caso, quando um aumenta, o outro diminui, então podemos escrever:
No nosso caso, o deslocamento é , então, temos:
Analisando o desenho do manômetro, como temos um lado que subiu uma distância e outro lado que abaixou uma distância , então a diferença entre as cotas é:
Passo 3
Agora vamos retornar à equação de Bernoulli e substituir as expressões conhecidas:
Resolvendo a integral, temos:
Agora vamos substituir o valor de encontrado no passo 2:
Dividindo a equação por , chegamos em: