Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 88

A água escoa a uma vazão de 0,025 m³/s em um tubo horizontal cujo diâmetro aumenta de 6 cm a 11 cm por uma seção de alargamento. Se a perda de carga na seção de alargamento é de 0,45 m e o fator de correção da energia cinética na entrada e na saída é de 1,05, determine a variação da pressão.

Passo 1

Oi pessoal, tudo bem?

Bem, assumimos inicialmente que:

1. O fluxo através do tubo é constante e incompressível.

2. O tubo é horizontal.

3. A energia cinética fatores de correção são dados como α 1 = α 2 = α =   1,05 .

E devemos lembrar que:

ρ á g u a = 1000 k g m 3

Passo 2

Pronto, agora vamos analisar o problema, ok?

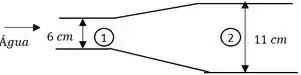
Tomamos os pontos 1 e 2 na entrada e saída da seção de ampliação ao longo da linha central do tubo. Observando que z 1 = z 2 , a equação de energia para um volume de controle entre esses dois pontos (em termos de cabeças) simplifica a:

P 1 ρ g + α 1 V 1 2 2 g + z 1 = P 2 ρ g + α 2 V 2 2 2 g + z 2 + h L               → P 2 - P 1 = ρ α V 1 2 - V 2 2 2 - ρ g h L               ( 1 )

Onde:

V 1 = V ˙ A 1 = 0,025 π 0,06 2 / 4 = 8,84 m s

V 2 = V ˙ A 2 = 0,025 π 0 , 11 2 / 4 = 2,63 m s

E h L representa a perda de carga.

Passo 3

Podemos, portanto, substituir os valores na equação 1, assim:

P 2 - P 1 = 1000 k g m 3 ⋅ 1,05 8,84 m / s ² ) - ( 2,63 m s 2 2 - 9,81 m s 2 ⋅ 0,45 m  

Resolvendo a equação, temos que:

P 2 - P 1 = 33   k P a

Resposta

Portanto: P 2 - P 1 = 33   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar atmosférico a 20°C entra e enche um tanque termicamente isolado, inicialmente evacuado. Usando uma análise de volume de controle da equação 3.63, calcule a temperatura do ar no tanque quando ele es
Ar escoa subsonicamente em um duto onde o atrito é negligenciado. Quando calor é adicionado em uma quantidade de 948 kJ/kg, a pressão cai de p 1 = 200k P a para p 2 = 106k P a . Usando a teoria unidim
Como as fórmulas para escoamento compressível em duto se compartam para quedas de pressão pequenas? Admita que o ar a 20°C entre em um tubo de 1 cm de diâmetro e 3 m de comprimento. Se f - = 0,028 com
Um observador ao nível do mar não ouve uma aeronave voando a 6000 m de altitude padrão até 15 segundos depois dela ter passado por ele. Estime a velocidade da aeronave.Bem, primeiramente como você est
Ar a 550 kPa e 100°C entra em um tubo liso de 1 m de comprimento e em seguida passa por um segundo tubo liso para um reservatório a 30 kPa, como na figura abaixo. Utilizando o diagrama de Moody para d