O escoamento compressível com atrito em um duto, Seção 9.7, supõe entalpia de estagnação e vazão em massa constantes, porém quantidade de movimento variável. Tal escoamento normalmente se denomina escoamento de Fanno, e uma linha representativa de todas as possíveis variações das propriedades em um diagrama temperatura- entropia denomina-se linha de Fanno. Admitindo um gás perfeito com k = 1,4 e os dados do Problema 9.86, desenhe uma curva de Fanno do escoamento para uma faixa de velocidades desde muito baixas () até muito altas (Ma >>1). Comente a respeito do significado do ponto de entropia máxima sobre essa curva.

Bora pra mais uma!

Relembrando do problema 9.86, na seção 1

com f=0,018. Podemos então calcular o número de Mach na seção 1, sendo e daí

Temos como equações básicas:

1. Energia:
2. Continuidade:
3. Entropia:

Simplesmente deixamos V variar de, por exemplo, 10m/s a 800m/s. Calculamos então as propriedades em (a, b, c), e plotamos um diagrama T versus s. Para isso, utilize a ferramenta de sua preferência, aqui utilizaremos o excel.

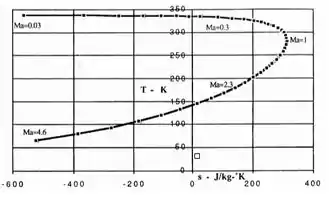
O resultado deste exercício forma uma linha de Fanno para este fluxo (imagem na resposta). Alguns números de Mach são explicitados, subsônicos na parte superior e supersônicos na parte inferior e os exatamente sônicos no lado direito (máxima entropia).