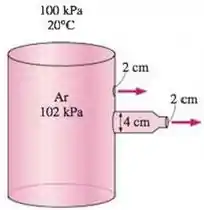
Um tanque muito grande contém ar a 102 kPa em um local onde o ar atmosférico está a 100 kPa e 20°C. Agora uma torneira com 2 cm é aberta. Determine a vazão máxima do ar através do orifício. Qual seria sua resposta se o ar fosse descarregado através de um tubo de 2 m de comprimento e 4 cm de diâmetro com um bocal de 2 cm de diâmetro? Você resolveria o problema da mesma forma se a pressão no tanque de armazenamento fosse 300 kPa?

Pronto, agora vamos analisar o problema, ok?

Assim, tomamos os pontos 1 no tanque e 2 logo na saída da torneira, ao longo da linha horizontal:

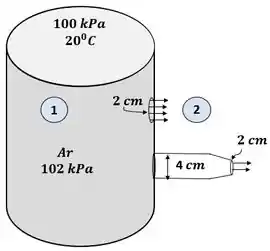
Feito essa análise, e observando que (ou, os efeitos de elevação são desprezíveis para gases), e , a equação de Bernoulli entre os pontos 1 e 2 fornece:

Porém, ainda não sabemos o para encontrar a velocidade na segunda seção.

Podemos, portanto, utilizar a equação geral dos gases para encontrar a densidade específica do ar, assim:

Assim, substituindo os valores na equação 1, temos:

Sabendo o valor da velocidade na saída da torneira, podemos encontrar a vazão através de:

A área da seção é expressa como:

Assim:

P.s: Esta é a vazão máxima, pois é determinada assumindo-se fluxo sem atrito. A vazão real será menor.

A adição de um tubo de 2 m de comprimento e 4 cm de diâmetro com um bocal de 2 cm de diâmetro não afetará a vazão, pois a vazão é sem atrito (usando a equação de Bernoulli, pode ser demonstrado que a velocidade nesta seção aumenta, mas a pressão diminui e há uma diferença de pressão menor para conduzir o fluxo através da aba, com efeito líquido nulo na taxa de descarga).

E se a pressão no tanque fosse de 300 kPa, o fluxo não é mais incompressível e, portanto, o problema nesse caso deve ser analisado usando a teoria do fluxo compressível.