Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 22

No Capítulo 9 discutiremos a equação diferencial para a conservação de massa, a equação da continuidade. Em coordenadas cilíndricas e para o escoamento em regime permanente

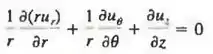
Escreva as dimensões primárias de cada termo aditivo da equação e certifique-se de que a equação é dimensionalmente homogênea. Mostre todo o seu trabalho.

Passo 1

Oi pessoal, tudo bem?

As dimensões primárias dos componentes de velocidade são . As principais dimensões das coordenadas , e as dimensões primárias da coordenada θ são adimensionais (θ é um ângulo sem dimensão).

Em resumo, somente relembramos as dimensões primárias de cada termo. Vamos agora ver se a equação é dimensionalmente homogênea.

Passo 2

Bem, relembrando, a equação é:

Assim, cada termo na equação pode ser escrito em termos de dimensões primárias:

Resposta

Portanto, foi provado que a equação é dimensionalmente homogênea.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de propagação de ondas superficiais de pequena amplitude em uma região de profundidade uniforme é dada por c 2 = σ ρ 2 π λ + g λ 2 π t a n h 2 π h λ em que h é a profundidade do líquido n

A inclinação da superfície livre de uma onda em regime permanente em um escoamento unidimensional em uma camada de líquido pouco profunda é descrito pela equação ∂ h ∂ x = - u g ∂ u ∂ x Use um escala

A equação que descreve a vibração de pequena amplitude de uma viga é ρ A ∂ 2 y ∂ t 2 + E I ∂ 4 y ∂ x 4 = 0 em que y é a deflexão da viga no local x e no tempo t , ρ e E são a massa específica e o módu

Em estudos atmosféricos, o movimento da atmosfera terrestre pode algumas vezes ser modelado com a equação D V _ D t + 2 Ω _× V _ = - 1 ρ ∇ p em que V _ é a velocidade de grande escala da atmosfera atr

Um escoamento bidimensional em regime permanente em um líquido viscoso é descrito pela equação: u ∂ u ∂ x = - g ∂ h ∂ x + μ ρ ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 Use uma escala de comprimento, L , e uma escala