Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 78
A água quente a uma temperatura média de 90°C flui através de uma seção de 15 m de um tubo de ferro fundido cujos diâmetros interno e externo são de 4 cm e 4,6 cm, respectivamente. A superfície externa do tubo, cuja emissividade é de 0,7, é exposta ao ar frio a 10°C no porão, com um coeficiente de transferência de calor de . O coeficiente de transferência de calor na superfície interna do tubo é de . Tomando as paredes do porão como sendo 10°C, determine também a taxa de perda de calor da água quente. Além disso, determine a velocidade média da água no tubo se a temperatura da água cair 3°C ao passar pelo porão.
Passo 1
Então galerinha, preparados??
O que temos aqui?
Nós temos um tubo, sem isolamento, contendo água quente no seu interior e um ambiente frio externo a ele.
Então teremos apenas três resistências, bora desenhar?
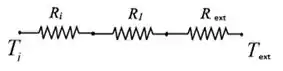
Então:
A resistência externa será composta de duas “partes”, não é?
A primeira, convectiva, e a segunda, radioativa. Sendo assim, o coeficiente externo será um coeficiente combinado entre os dois:
Bora reescrever então esta última resistência??
Já sabemos como calcular as resistências, só precisamos das áreas e do coeficiente de radioatividade.
Bora lá?
Passo 2
A área interna da seção transversal é dada por:
Para a área externa nós levamos em consideração o diâmetro externo do tubo:
Se já achamos a área agora vamos procurar o coeficiente de radiação.
Se lembram da fórmula?
Tabelado nós temos a constante de Boltz:
Sabemos que:
Não temos informação nenhuma sobre a temperatura da superfície externa do tubo, mas podemos assumir que elas estará um pouco mais fria do que a água que está passando dentro dele, certo?
Então vamos assumir que seja 80°C:
Agora é só substituir galerinha!!
Agora vamos dar sequência !!
Passo 3
Agora vamos substituir nas fórmulas e achar nossas tão queridas resistências:
Sabendo que podemos adaptar as resistências:
Substituindo:
Como estão todas em série, a resistência total é dada por:
Passo 4
Agora sim nós conseguimos saber qual será a perda de calor para o ambiente.
Usamos a fórmula do calor:
Substituindo:
Como a variação em graus Celsius e kelvin é a mesma:
Beleza! Achamos nossa primeira resposta!
Passo 5
A próxima pergunta é: Qual a velocidade média da água no tubo se a temperatura da água cair 3°C ao passar pelo porão?
Bom galera, antes de qualquer coisa, como achamos a velocidade de um fluido?
Para isso tem uma fórmula bem simples:
A densidade da água nós sabemos porque já é tabelado:
E a área aqui deve ser calculada como a área da seção circular interna:
Como
Agora nós só precisamos achar o fluxo mássico de água que atravessa o tubo.
Passo 6
Como faremos para achar o fluxo mássico??
Simples!!
Sabemos que:
Na fórmula:
Temos todos os dados para achar a velocidade, então é só substituir na equação do passo 5!
Passo 7
Baseamos todos os nossos cálculos na suposição que a temperatura da superfície externa do tubo é de 80°C, então precisamos confirmar.
Para isso vamos usar a fórmula do calor levando em conta somente a resistência apresentada pela convecção interna e pelo tubo
Substituindo:
Bem próximo do valo que assumimos, então não precisamos repetir nossos cálculos!
De boa, galerinha?!
Tranquilinha?
Resposta
Calor Perdido:
Velocidade: