Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 87
Um tanque com um orifício reentrante chamado bocal de Borda é mostrado. O fluido é não viscoso e incompressível. O orifício reentrante essencialmente elimina o escoamento o longo das paredes do tanque, de modo que a pressão ali é aproximadamente hidrostática. Calcule o coeficiente de contração, . Sugestão: Equacione a força de pressão hidrostática e a quantidade de movimento do jato.
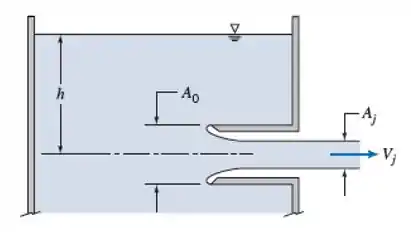
Passo 1
Vamos começar o exercício ilustrando o volume de controle que vamos utilizar:
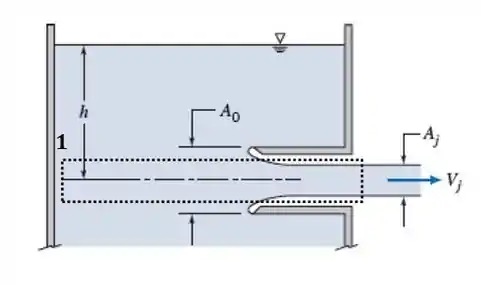
Vamos começar o exercício aplicando Bernoulli entre o ponto 1 e a saída do jato (ponto 2), dessa forma, temos:
Nesse caso os dois pontos estão a mesma altura, então podemos desprezar a diferença entre as cotas e . E como a saída está exposta a atmosfera, então temos e dessa forma iremos obter uma pressão manométrica. Temos ainda, considerando um tanque de grandes dimensões, que a velocidade no ponto 1 é zero. Então, reescrevendo a equação, temos:
Passo 2
Agora, da hidrostática, sabemos que a pressão no ponto 1 pode ser dada pela altura da coluna de água, que nesse caso é , então, temos:
Igualando essa expressão à equação encontrada para no passo 1, temos:
Passo 3
Agora vamos aplicar o equilíbrio de momento, da equação 4.18a, para o sistema, a equação tem a forma:
Nesse exercício, como temos regime permanente, então podemos desconsiderar o termo com a derivada no tempo. Iremos desprezar também as forças de campo na direção , de modo que . Então a equação se torna:
Nesse exercício, temos . Sabemos que , que é a força exercida pela coluna da água, pode ser encontrada multiplicando o valor da pressão nesse ponto pelo valor da área, então, temos:
E, como vimos no passo 2, podemos escrever , então se torna:
Substituindo esses valores na equação de cima, temos:
Passo 4
Agora vamos igualar as duas equações encontradas para nos passos 2 e 3, então, temos: