Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 191
Aletas circulares de seção transversal uniforme, com diâmetro de 10 mm e comprimento de 50 mm, são fixadas em uma parede com temperatura na superfície de 350 °C. As aletas são feitas de material com condutividade térmica de 240 e são expostas ao ar ambiente condicionado de 25 °C, e o coeficiente de transferência de calor por convecção é . Determine a taxa de transferência de calor e trace a variação de temperatura da única aleta para as seguintes condições de contorno:
- Aleta infinitamente longa
- Aleta de ponta adiabática
- Aleta com temperatura na ponta de 250 °C
- Convecção na ponta da aleta
Passo 1
Começamos a questão deixando claro quais são as nossas hipóteses para o problema. Neste caso, temos condução de calor unidimensional e em regime permanente, propriedades térmicas constantes e é desconsiderado o efeito da radiação.
Para esta questão, vamos calcular a taxa de transferência de calor e indicar a equação para a variação de temperatura para cada item primeiramente. Somente ao final dela, iremos traçar em um gráfico todas as distribuições de temperatura.
Portanto, vamos começar determinando parâmetros geométricos necessários para calcularmos o que a questão nos pede. Começando pelo perímetro e área da aleta, temos:
Continuando com outros parâmetros, temos:
Agora já determinarmos os parâmetros que utilizaremos em todos os casos que a questão nos pede.
Passo 2
Vamos começar calculando a taxa de transferência de calor em uma aleta infinitamente longa. Para isto, a fórmula que devemos utilizar é:
Já a distribuição de temperatura é dada pela seguinte fórmula:
Substituindo os valores e isolando , temos:
E esta é a equação para uma aleta infinitamente longa.
Passo 3
Agora, vamos para o caso de uma superfície com ponta adiabática. Para isto, a fórmula que devemos utilizar é:
Já a distribuição de temperatura é dada pela seguinte fórmula:
Substituindo os valores e isolando , temos:
E esta é a equação para uma aleta com ponta adiabática.
Passo 4
Agora, vamos para o caso de uma superfície com temperatura fixa na ponta. Para isto, a fórmula que devemos utilizar é:
Já a distribuição de temperatura é dada pela seguinte fórmula:
Substituindo os valores e isolando , temos:
E esta é a equação para uma aleta com ponta temperatura constante na ponta.
Passo 5
O último caso a analisarmos é a aleta com convecção na ponta. Para isto, a fórmula que devemos utilizar é:
Já a distribuição de temperatura é dada pela seguinte fórmula:
Substituindo os valores e isolando , temos:
E esta é a equação para uma aleta com convecção na ponta.
Passo 6
Para finalizarmos a questão, vamos traçar as variações de temperatura para cada um dos casos estudados aqui nesta questão. Desta forma, temos o seguinte gráfico:
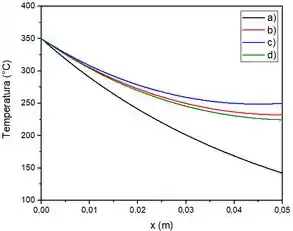
E assim, finalizamos a questão!
Resposta
- Para uma aleta infitamente longa, a taxa de transferência de calor é:
- Para uma aleta com ponta adiabática, a taxa de transferência de calor é:
- Para uma aleta com temperatura fixa na ponta, a taxa de transferência de calor é:
- Para uma aleta com convecção na ponta, a taxa de transferência de calor é:
Para finalizarmos, temos o esboço da variação de temperatura para cada um dos casos estudados:
