Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 106

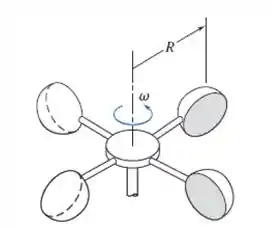
Um anemômetro para medir velocidade do vento é fabricado com quatro taças hemisféricas de 50 mm de diâmetro, conforme mostrado. O centro de cada taça é colocado a uma distância R = 80 mm do pivô. Determine a constante de calibração teórica k na equação de calibração V = kω, em que V (km/h) é a velocidade do vento e ω (rpm) é a velocidade de rotação. Em sua análise, baseie os cálculos do torque no arrasto gerado no instante em que duas taças estão ortogonais e as outras duas estão paralelas, e ignore o atrito nos mancais. Explique por que, na ausência de atrito, para uma dada velocidade do vento, o anemômetro gira com velocidade constante em vez de acelerar continuamente. Se o mancal do anemômetro real tem atrito (constante) tal que o anemômetro necessita de uma velocidade mínima do vento de 1 km/h para começar a girar, compare as velocidades de rotação com e sem atrito, para V = 10 km/h.

Passo 1

Beleza! Então, para começar esse exercício, vamos escrever a equação para o coeficiente de arrasto:

C D = F D 1 2 ρ V 2 A

Então a força de arrasto será dada por:

F D = C D ρ V 2 A 2 = C D ρ V 2 π D 2 8

Agora vamos recorrer à tabela 9.3 para pegar os coeficientes de arrasto para o nosso problema:

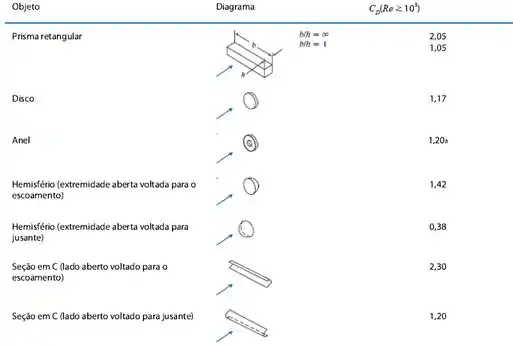
Então, a taça com a extremidade aberta voltada para o escoamento terá:

C D 1 = 1,42

E, para a extremidade aberta voltada para jusante será:

C D 2 = 0,38

Passo 2

Agora, para resolver o problema vamos considerar que temos regime permanente e que a velocidade do vento é constante em todos os pontos. Dessa forma, o somatório dos momentos será sempre zero. As duas taças que estão paralelas ao escoamento não irar gerar momento. As duas taças abertas, uma voltada para o escoamento e a outra não, vão exercer momento devido às forças de arrasto. Então, o somatório de momento resultante será:

1 2 ρ A V - R ω 2 C D 1 R - 1 2 ρ A V + R ω 2 C D 2 R = 0 → V - R ω 2 C D 1 = V + R ω 2 C D 2

Então, como nos foi dado no enunciado que:

k = V ω

Então, reescrevendo a equação acima para esse termo aparecer, temos:

V ω - R 2 C D 1 = V ω + R 2 C D 2 → k - R 2 C D 1 = k + R 2 C D 2

k - R 2 k + R 2 = C D 2 C D 1 → k - R k + R = C D 2 C D 1 → k - R = k + R C D 2 C D 1

k = k C D 2 C D 1 + R C D 2 C D 1 + R → k 1 - C D 2 C D 1 = R 1 + C D 2 C D 1  

k = R 1 + C D 2 C D 1 1 - C D 2 C D 1

Então, substituindo os valores conhecidos, temos:

k = 0,08 1 + 0,38 1,42 1 - 0,38 1,42 → k = 0,2515   m

Passo 3

No entanto, para o caso real, precisamos também considerar o torque produzido quando o anemômetro está parado, mas na iminência de se mover. Nesse caso, temos que a velocidade mínima do vento é:

V = 1   k m / h

O torque produzido para essa velocidade de vento será:

T = ρ A V m í n 2 C D 1 2 R - ρ A V m í n 2 C D 2 2 R = ρ π D 2 V m í n 2 C D 1 2 R - ρ π D 2 V m í n 2 C D 2 2 R

Substituindo os valores conhecidos, chegamos em:

T = 1,23 π 0,05 2 1 3,6 2 1,42 2 0,08 - 1,23 π 0,05 2 1 3,6 2 0,38 2 0,08

T = 4,23.10 - 5 - 1,133.10 - 5 → T = 3,1.10 - 5   N . m

Então, agora, aplicando novamente o equilíbrio de momento igual fizemos no passo 2, temos:

1 2 ρ A V - R ω 2 C D 1 R - 1 2 ρ A V + R ω 2 C D 2 R - T = 0

V - R ω 2 C D 1 - V + R ω 2 C D 2 = 2 T ρ R A

V - R ω 2 C D 1 - V + R ω 2 C D 2 = 8 T ρ R π D 2

Para resolver essa equação para ω , precisamos utilizar um sistema computacional, então, chegaremos em:

10 3,6 - 0,08 ω 2 1,42 - 10 3,6 + 0,08 ω 2 0,38 = 8 3,1.10 - 5 1,23 0,08 π 0,05 2 → ω = 10,56   r a d / s

E, para o caso sem atrito, temos que a rotação será:

ω s a = V k = 10 3,6 0,2515 → ω s a = 11,04   r a d / s

Resposta

ω = 10,56   r a d / s

ω s a = 11,04   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The Toyota Prius has a drag coeffi cient of 0.25, a frontalarea of 23.4 ft2, and an empty weight of 3042 lbf. Its rollingresistance coefficient is Crr 5 0.03, that is, the rolling resistance is 3 perc
The world record for automobile mileage, 12,665 miles pergallon, was set in 2005 by the PAC-CAR II in Fig. P7.109,built by students at the Swiss Federal Institute of Technology in Zurich [52]. This li
The movie The World’s Fastest Indian tells the story ofBurt Munro, a New Zealander who, in 1967, set a motorcycle record of 201 mi/h on the Bonneville Salt Flats.Using the data of Prob. P7.74, (a) est
A sea-level smokestack is 52 m high and has a square crosssection. Its supports can withstand a maximum side forceof 90 kN. If the stack is to survive 90-mi/h hurricane winds,what is its maximum possi
For those who think electric cars are sissy, Keio University inJapan has tested a 22-ft-long prototype whose eight electricmotors generate a total of 590 horsepower. The “Kaz” cruisesat 180 mi/h (see