Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 92
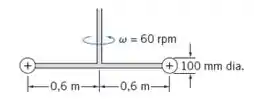
Um misturador rotativo é construído com dois discos circulares, conforme mostrado. O misturador é acionado a 60 rpm dentro de um grande vaso contendo uma solução de salmoura (SG = 1,1). Despreze o arrasto sobre as hastes e o movimento induzido no líquido. Estime o torque e a potência mínimos requeridos para acionar o misturador.
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que, por definição:
Também sabemos que:
Desprezando-se o atrito nas hastes, a velocidade do disco será dada por:
Da tabela 9.2, tiramos que .
Já a área do disco, será:
Substituindo:
Portanto, a força de arrasto será:
Portanto, podemos substituir para achar o torque e a potência:
Resposta
Exercícios de Livros Relacionados
Considere um mastro de bandeira cilíndrico de altura H . Para coeficiente de arrasto constante, avalie a força de arrasto e o momento fletor sobre o mastro, se a velocidade do vento varia como u / U=(
Uma bola de hockey tem diâmetro D=73m m e massa m=160g . Quando bem golpeada, ela parte do bastão com velocidade inicial U 0=50m / s . A bola é essencialmente lisa. Estime a distância percorrida em tr
O Problema 9.107 mostrou um disco circular pendurado em uma corrente de ar por meio de uma haste cilíndrica. Considere que a haste tem L=40m m de comprimento e d=3m m de diâmetro. Resolva o Problema 9
Uma bola de tênis, com massa de 57g e diâmetro 64m m , é solta em arpadrão ao nível do mar. Calcule a velocidade terminal da bola. Considerando, como uma aproximação, que o coeficiente de arrasto perm
Uma pequena esfera ( D=6m m ) é observada cair, com uma velocidade terminal de 60m m / s , através de óleo de rícino. A temperatura é 20 ° C . Calcule o coeficiente de arrasto para a esfera. Determine