Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 5

Num viscosímetro de esfera, uma esfera de aço de massa específica ρ = 7.800   k g / m 3 e diâmetro 1   m m afunda num líquido de massa específica ρ = 800   k g / m 3 , com uma velocidade limite de 2   c m / s . Calcular a viscosidade cinemática do fluido.

Passo 1

Os dados da questão:

  • Densidade da esfera: ρ a ç o = 7.800   k g / m 3
  • Diâmetro da esfera: d = 1   m m = 0,001   m
  • Densidade do líquido: ρ l i q u i d o = 800   k g / m 3
  • Velocidade da esfera: v 0 = 2   c m / s = 0,02   m / s    

A questão pede:

  • Viscosidade cinemática do fluido: ν = ?

    • Vamos considerar:

  • Gravidade g = 10   m / s

    • Passo 2

    A esfera imersa em fluido está caindo puxada pela força peso P. O movimento para baixo gera uma força de arrasto F a para cima. Além disso, uma força de flutuação E também atua sobre a esfera. A situação é desenhada abaixo:

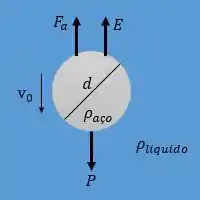
    Vamos considerar a situação em que a esfera já atingiu velocidade terminal, ou seja, não está acelerando. Então temos que:

    ∑ F y = 0 ⇒ F a + E - P = 0

    Logo:

    P = F a + E

    Passo 3

    Sabemos que:

  • Empuxo sobre a esfera é: E = ρ l i q u i d o ⋅ g ⋅ V e s f e r a
  • O peso da esfera é: P = V e s f e r a ⋅ ρ a ç o ⋅ g
  • A força de arrasto é dada por: F a = C a ⋅ ρ l i q u i d o ⋅ v 0 2 2 A

Aplicando essas equações:

P = F a + E

V e s f e r a ⋅ ρ a ç o ⋅ g = C a ⋅ ρ l i q u i d o ⋅ v 0 2 2 A + ρ l i q u i d o ⋅ g ⋅ V e s f e r a

1 6 π d 3 ⋅ ρ a ç o ⋅ g = C a ⋅ ρ l i q u i d o ⋅ v 0 2 2 ⋅ π d 2 4 + ρ l i q u i d o ⋅ g ⋅ 1 6 π d 3

Aplicando os valores:

1 6 π ⋅ ( 0,001 ) 3 ⋅ 7800 ⋅ 10 = C a ⋅ 800 ⋅ 0,02 2 2 ⋅ π ⋅ 0,001 2 4 + 800 ⋅ 10 ⋅ 1 6 π ⋅ 0,001 3

13 π ⋅ 10 - 6 = 4 π ⋅ 10 - 8 ⋅ C a + 4 3 π ⋅ 10 - 6

C a = 13 ⋅ 10 - 6 - 4 3 ⋅ 10 - 6 4 ⋅ 10 - 8

Resolvendo:

C a = 292

Passo 2

Com o valor do coeficiente de arrasto, podemos calcular o número de Reynolds. Como este é um escoamento lento (apenas 2   c m / s ), podemos usar:

C a = 24 R e

R e = 24 292

Passo 3

Para concluir a questão, vamos usar o número de Reynolds para calcular a viscosidade:

R e = v 0 ⋅ d ν

ν = v 0 ⋅ d R e

ν = 0,02 ⋅ 0,001 24 292

ν = 2,43 ⋅ 10 - 4 m 2 s

Convertendo:

ν = 2,43 c m 2 s

Resposta

ν = 2,43 c m 2 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 9.46, porém agora considere que o escoamento de água é a 10m / s (use as fórmulas para o C D da Seção 9.7).
Uma barcaça de fundo chato, de 24m de comprimento e 10,7m de largura, submersa até uma profundidade de 1,5m , deve ser rebocada rio acima (a água do rio está a 15,5 ° C ) . Estime e plote a potência r
Um rebocador de barcaças fluviais é testado em um tanque de provas. O modelo do rebocador é construído em uma razão de escala de 1 : 13,5 . As dimensões do modelo são: comprimento total 3,5m , través
Como parte das comemorações do bicentenário da independência, em 1976, um grupo empreendedor pendurou uma gigantesca bandeira norte-americana ( 59m de altura e 122m de largura) nos cabos de suspensão
Você é chamado pela equipe de canoagem do Flamengo para estimar o arrasto de atrito superficial sobre a canoa de competição de oito lugares com patrão. O casco da canoa pode ser aproximado como um mei