Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 17

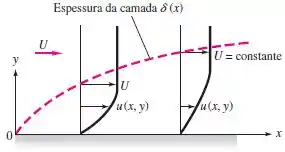
Uma aproximação razoável para a camada-limite laminar incompressível bidimensional sobre a superfície plana da Figura P 4.17 é

u = U 2 y δ - y 2 δ 2   p a r a   y ≤ δ   e m   q u e   δ = C x 1 2 ,   C = c o n s t

(a) Admitindo uma condição de não escorregamento na parede, encontre uma expressão para o componente de velocidade y   x ,   y para y ≤ δ . (b) Depois encontre o valor máximo de v em x = 1   m , para o caso particular do escoamento de ar, quando U = 3   m / s e δ = 1,1   c m .

Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

a)

Para resolvermos isso vamos encontrar a equação da continuidade para um sistema de duas coordenadas, algo que já fizemos bastante até agora, vamos lá!

d v d y = - d u d x

d v d y = - d d x U 2 y δ - y 2 δ 2

Agora vamos lembrar que:

δ = C x 1 2

Assim:

d v d y = - d d x U 2 y δ - y 2 δ 2

d v d y = - U - 2 y δ 2 + 2 y 2 δ 3 d d x C x  

Agora calculando v :

v = 2 U δ 2 x ∫ 0 y y δ 2 - y 2 δ 3 d y

v = 2 U δ 2 x y 2 2 δ 2 - y 3 3 δ 3

Passo 2

b)

Agora para matarmos essa questão de vez!

Podemos observar que v aumenta como uma função monótona de acordo com o crescimento de y , assim v m á x ocorre em y = δ , fazendo nossas continhas:

v m á x = 2 U δ 2 x δ 2 2 δ 2 - δ 3 3 δ 3 = δ U x 1 6

v m á x = δ U 6 x = 3   m s ⋅ 0,011 6 ⋅ 1 m

v m á x = 0,0055   m / s  

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

a)

v = 2 U δ 2 x y 2 2 δ 2 - y 3 3 δ 3

b)

v m á x = 0,0055   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a distribuição de velocidade em coordenadas polares planas v r = C r v θ = K rv z = 0 em que C e K são constantes. (a) Determine se a equação da continuidade é satisfeita. (b) Fazendo o esbo
Um pistão comprime gás em um cilindro movendo-se a uma velocidade constante V , como na Figura P 4.18 .Admita que a massa específica do gás e a posição do pistão em t = 0 sejam ρ 0 e L 0 , respectivam
Um campo de velocidade incompressível bidimensional tem u = K ( 1 - e - a y ) , para x ≤ L e 0 ≤ y ≤ ∞ . Qual é a forma mais geral de v ( x ,y ) para a qual a continuidade é satisfeita e v = v 0 em y
O ar escoa sob condição permanente, aproximadamente unidimensional, por um bocal cônico na Figura P4.21. Se a velocidade do som é aproximadamente 340 m/s, qual é a razão mínima de diâmetros do bocal D