Um pistão comprime gás em um cilindro movendo-se a uma velocidade constante , como na Figura .

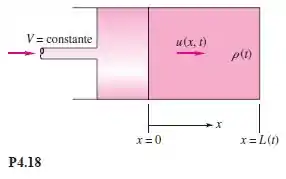
Admita que a massa específica do gás e a posição do pistão em sejam e , respectivamente. Considere que a velocidade do gás varie linearmente de na face do pistão até em . Se a massa específica do gás varia apenas com o tempo, encontre uma expressão para .

E aí, tudo bem? Bora matar essa questão rapidinho!

Nosso sistema é unidimensional, então lembrando que a equação da continuidade fica nesta forma:

Onde:

Assim nossa equação da continuidade fica com essa forma:

Separando as variáveis e integrando:

Ou:

Aplicando a esponencial dos dois lados vamos ter a seguinte equação:

Pra finalizar:

Isso é tudo pessoal, conseguimos mais uma! \o/