Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 16

Considere a distribuição de velocidade em coordenadas polares planas

v r = C r                 v θ = K r                   v z = 0

em que C e K são constantes. (a) Determine se a equação da continuidade é satisfeita. (b) Fazendo o esboço de algumas direções do vetor velocidade, faça um gráfico de uma única linha de corrente para C = K . O que esse campo de escoamento pode simular?

Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

a)

Vamos resolver essa questão, mas vamos usar a equação 4.12 b em coordenadas polares, assim:

1 r ∂ ∂ r r v r + 1 r ∂ ∂ r r v θ = 0

1 r ∂ ∂ r r C r + 1 r ∂ ∂ r r K r = 0

1 r ∂ ∂ r C + 1 r ∂ ∂ r K = 0

0 + 0 = 0

A equação da continuidade é satisfeita!

Passo 2

b)

Agora para matarmos essa questão de vez!

Fazendo uma conta grosseira para C = K , podemos checar o seguinte:

∫ V = ∫ C r d r + ∫ C r d θ

∫ V = C ⋅ ln ⁡ r + θ r

Considerando que r é função de θ temos uma função espiral, com característica logarítmica, vamos fazer um esboço disso, assim temos:

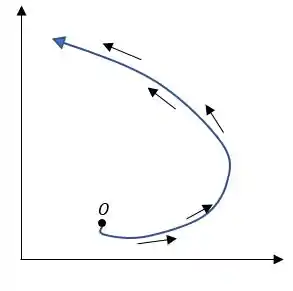
Esse tipo de escoamento é comumente utilizado para a simulações de tornados! :o

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

a)

A equação da continuidade é satisfeita!

b)

gráfico vide passo-a-passo, pode simular tonardos!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o escoamento no bocal convergente da Figura P 4.2 tenha a forma V = V 0 [ 1 + ( 2 x ) / L] i . Calcule (a) a aceleração do fluido em x =L e (b) o tempo necessário para uma partícula de flu
Um campo de velocidade bidimensional é dado por u = - K y x 2 + y 2v = K x x 2 + y 2 em que K é constante. Esse campo satisfaz a continuidade incompressível? Transforme essas velocidades em componente
As coordenadas polares esféricas ( r ,θ ,ϕ ) são definidas na Figura P 4.12 . As transformações cartesianas são x = r sen ⁡ θ cos ⁡ ϕ y = r sen ⁡ θ sen ⁡ ϕ z = r cos ⁡ θ A relação da continuidade cart
Um campo de velocidade bidimensional é dado por V = x 2 - y 2 + x i - ( 2 x y + y ) j em unidades arbitrárias. Em x ,y = ( 1 ,2 ) , calcule (a) as acelerações a x e a y , (b) o componente de velocidad
Um campo de velocidade idealizado é dado pela fórmula V = 4 t xî - 2 t 2 yj ^ + 4 x zk ^ î Esse campo de escoamento é permanente ou não permanente? Ele é bidimensional ou tridimensional? No ponto x ,y