Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 52
Ar-padrão escoa da atmosfera para dentro de um canal plano, largo, conforme mostrado. Camadas limite laminares formam-se sobre as paredes de topo e de fundo do canal (ignore efeitos de camada limite sobre as paredes laterais). Considere que as camadas limite comportam-se como sobre uma placa plana, com perfis lineares de velocidade. Em qualquer distância axial a partir da entrada, a pressão estática é uniforme na seção transversal do canal. Considere escoamento uniforme na seção (1). Indique onde a equação de Bernoulli pode ser aplicada neste campo de escoamento. Determine a pressão estática (manométrica) e a espessura de deslocamento na seção (2). Trace a pressão de estagnação (manométrica) através do canal da seção (2), e explique o resultado. Determine a pressão estática (manométrica) na seção (1) e compare com a pressão estática (manométrica) na seção (2).
Passo 1
Vamos listar o que a gente precisa achar:
- Equação de Bernoulli para esse escoamento
- Pressão estática (manométrica) na seção (2)
- Expessura de deslocamento na seção (2)
- Relação entre a pressão de estagnação e a altura () de um ponto na seção (2).
- Pressão estática na seção (1)
E enunciado dá umas informações para gente:
- Temos um perfil de velocidade linear em (2):
- largura:
- expessura de perturbação:
- velocidade de corrente livre:
- altura do canal:
- ar-padrão: e
Vamo começar!
Passo 2
A equação de Bernoulli tem essa carinha:
A gente pode usar ela tanto antes do ar entrar no canal, quanto depois, dentro da região onde não há efeitos de viscosidade.
Passo 3
Vamos começar achando a expessura de deslocamento na seção (2). Para o perfil de velocidade linear, temos que:
Daí a gente tira que:
Passo 4
Para achar as pressões estáticas nas seções, vamos precisar das velocidades em cada seção. A gente consegue encontrar as que faltam pela conservação de massa, a vazão da seção (1) deve ser igual a da :
Mas repara que na seção dois, a gente considera que a nossa seção onde a velocidade é uniforme é menor porque tem a presença de camadas limite. Por isso a gente vai usar a expessura de deslocamento para achar essa nova área.
Aí nossas continhas ficam assim:
Com a conservação de massa:
Passo 5
Para achar a pressão estática na seção (1), vamos usar a equação de Bernoulli entre o lado de fora e a própria seção:
Mas para achar a pressão manométrica:
Passo 6
Para achar a pressão estática na seção (2), vamos usar a equação de Bernoulli entre o lado de fora e a própria seção:
Mas para achar a pressão manométrica:
Deu meno que a da seção (1), isso ocorre porque a velocidade vai aumentando ao longo do canal por causa da diminuição de seção devido as camadas limite.
Passo 7
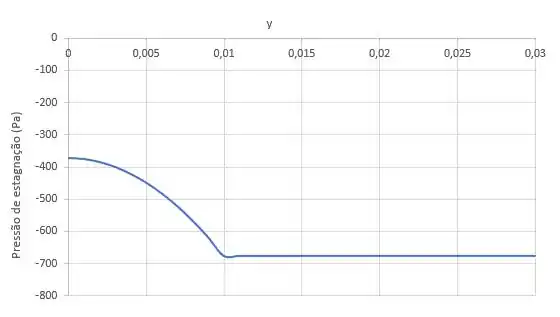
Falta a gente traçar o gráfico da pressão de estagnação em (2).Ela é simétrica horizentalmente. Podemos dizer que ela vai ser a soma da pressão estática com a dinâmica:
Lembrando que:
A gente pode substituir e ficar com essa expressão para traçar o gráfico:
Como sabemos o valor de e , conseguimos esboçar esse gráfico.
Um último detalhe: a gente sabe que onde não há camada limite, a velocidade é uniforme , por isso essa expressão só vai servir para .
Enquanto de ,
Passo 8
Nosso gráfico fica com essa cara:
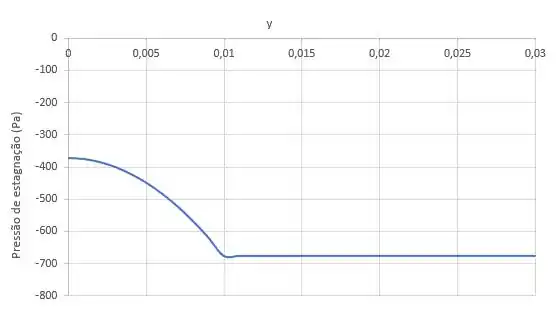
Ela é um indicativo de energia mecânica total. A gente vê que perto das paredes há perda de energia, mas na região central não tem.
Resposta
