Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 137

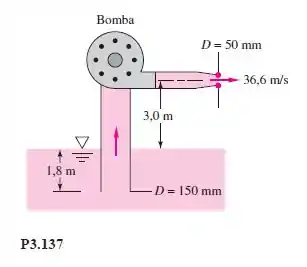
Um barco anti-incêndio retira água do mar (d = 1,025) por um tubo submerso e a descarrega através de um bocal, como na Figura P3.137. A perda de carga total é de 2 m. Se a eficiência da bomba é de 75%, qual a potência requerida do motor, em hp, para acionar a bomba?

Passo 1

Bora pra mais uma!!

Primeiramente, vamos as hipóteses sobre o nosso sistema de controle, que será todo o esboço da imagem:

  1. Regime permanente
  2. Fluido incompressível

Agora, vamos definir alguns pontos para aplicar a equação de energia. O primeiro ponto (1) será a superfície do mar e o segundo ponto (2) será o bocal de descarga após a bomba.

Então, temos a equação de energia:

P 1 ρ g + V 1 2 2 g + Z 1 = P 2 ρ g + V 2 2 2 g + Z 2 + h p - h b o m b a

Note que, as pressões são idênticas (pressão atmosférica), e a velocidade 1, é nula, visto que o nível do mar não diminuirá muito, daí:

h b o m b a = V 2 2 2 g + Z 2 - Z 1 + h p

h b o m b a = 36,6 m s 2 2 g + 3 m + 2 m = 73,35 m

Passo 2

Agora, vamos descobrir a potência requerida, para isso vamos começar calculando a vazão.

Q = V * A = 36,6 m s * 0,05 m 2 2 * π = 0,072 m 3 s .

Daí, a potência será definida pela seguinte expressão:

P b o m b a = ρ g Q h b o m b a η b o m b a = 1,025 * 998 k g m 3 * 9,8 m s 2 * 0,072 m 3 s * 73,35 m 0,75 = 70591,41 W

Por fim, vamos converter para a unidade pedida no enunciado:

P b o m b a = 70,59141 k W * 1 h p 0,746 k W = 94,627 h p .

Resposta

A potência requerida do motor é de 94,627 h p .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O campo de velocidade para um dipolo plano é dado na Tabela 6.2. Se ∧ = 3m 3 . s - 1 , a massa específica do fluido é ρ = 1,5k g / m 3 e a pressão no infinito é 100 kPa, trace um gráfico da pressão ao
Um velho truque de mágica é feito com um carretel vazio e uma carta de baralho. A carta é apoiada contra o fundo do carretel. Contrariamente à intuição, quando alguém sopra para baixo através do orifí
Um objeto, com superfície inferior plana, move-se para baixo com velocidade U = 1,5m / s dentro do jato de líquido do Problema 4.81. Determine a pressão mínima de suprimento necessária para produzir o
Um jato de ar, horizontal e assimétrico, com 10 mm, de diâmetro, atinge um disco vertical de 190 mm de diâmetro. A velocidade do jato é 69 m/s na saída do bocal. Um manômetro é conectado ao centro do
Um jato de água é direcionado para cima a partir de um bocal bem projetado com área A 1 = 600m m 2 , a velocidade do jato na saída é V 1 = 6,3m / s . O escoamento é em regime permanente e a corrente d