Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 15

Eixos de aço-carbono ( A I S I   1010 ) com 0,1   m de diâmetro são tratados termicamente pelo aquecimento em fornalhas a gás onde os gases se encontram a 1200   K e mantêm um coeficiente convectivo de 100 W m 2   ·   K . Se os eixos entram no forno a 300   K , quanto tempo eles devem permanecer no interior da fornalha para que suas linhas de centro atinjam a temperatura de 800   K ?

Passo 1

Vamos lá! Nosso problema nos pede o tempo necessário pro centro do eixo atingir a temperatura desejada, mas antes que tal desenharmos o comportamento desse problema pra entendermos o que o ocorre. Fica assim.

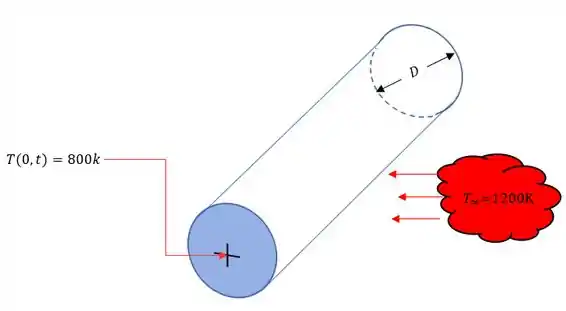
Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - C o n d u ç ã o   s o m e n t e   n o   s e n t i d o   r a d i a l

Passo 2

Vamos lá nosso problema nos pede o tempo necessário pra atingir a temperatura, T = 800 K , para isso vamos usar os dados da tabela A . 1 para o aço A I S I   1010 , vamos calcular primeiro o número de B i o t para verificarmos a condição de capacitância global do sistema:

B i = h r 2 k = 100 W m 2 ⋅ K ⋅ 0,05   m 2 ⋅ 51,2 W m ⋅ K = 0,048

Como B i ≪ 0,1 temos que podemos afirmar que a condição de capacitância global é válida e usarmos a equação 5.6 para encontrarmos o tempo, assim:

T - T ∞ T i - T ∞ = e - A s h ρ V c t

Aplicando a função l n nos dois lados da equação temos

ln ⁡ T - T ∞ T i - T ∞ = - 4 h D ρ c t

ln ⁡ 800 K - 1200 K 300 K - 1200 K = - 4 ⋅ 100 W m 2 ⋅ K 7832 k g m 3 ⋅ 541   J k g ⋅ K ⋅ 0,1   m t

t = 859   s

Passo 3

Só pra título de curiosidade podemos analisar a diferença do nosso resultado encontrado pro valor real usando a aproximação pela equação 5.52

T - T ∞ T i - T ∞ = C 1 e - ς 1 2 F 0

Sendo B i = h D 2 k = 0,0976 , a tabela 5.1 nos indica, C 1 = 1,024 e ς 1 = 0,436 , assim nossa equação fica:

- 400 - 900 = 1,024 ⋅ e - 0,436 2 ⋅ 1,2 ⋅ 10 - 5 0,05 ⋅ t

Aplicando o l n em ambos os lados temos:

ln ⁡ 0,434 = - 0,436 2 ⋅ 1,2 ⋅ 10 - 5 0,05 ⋅ t

t = 915   s

Logo t tem uma margem de erro de 6 % , logo a consideração de capacitância global nos leva a subestimar o tempo real para atingir a temperatura de 800 K no centro do eixo

Isso é tudo pessoal!

Resposta

t = 915   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma chapa de alumínio de espessura de 10c m ( ρ = 2.702k g / m 3 ,c p = 903J / k g ⋅ K ,k = 237W / m ⋅ Keα = 97,1 × 10 - 6m 2 / s ) é aquecida em líquido com temperatura de 500 ℃ ℃. A placa de alumíni
Batatas brancas ( k = 0,50W / m ⋅ Keα = 0,13 × 10 - 6m 2 / s ) com diâmetro médio de 6c m , inicialmente a uma temperatura uniforme de 25 ℃ ℃, devem ser resfriadas por ar refrigerado a 2 ℃ ℃ fluindo a
Uma barra longa de pirocerâmica ( ρ = 2.600k g / m 3 ,c p = 808J / k g ⋅ K ,k = 3,98W / m ⋅ Keα = 1,89 × 10 - 6m 2 / s ) com diâmetro de 10m m tem uma temperatura inicial de 1.000 ℃ ℃. A barra de piro
Frangos com massa média de 1,7k g( k = 0,45W / m ⋅ Keα = 0,13 × 10 - 6m 2 / s ) , inicialmente a uma temperatura uniforme de 15 ℃ ℃, devem ser resfriados em salmoura agitada a - 7 ℃ ℃. O coeficiente m
Uma placa de pirocerâmica ( ρ = 2.600k g / m 3 ,c p = 808J / k g ⋅ K ,k = 3,98W / m ⋅ Keα = 1,89 × 10 - 6m 2 / s ) de 6m m de espessura está sendo resfriada em uma sala com temperatura do ar de 25 ℃ ℃