Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 25
Bolas de aço de carbono de de diâmetro são recozidos por aquecimento a em forno e, depois, esfriadoas lentamente até no ar ambiente a . Se o coeficiente médio de transferência de calor é , determine o tempo de demora do processo de recozimento. Considerando que bolas devem ser recozidas por hora, determine a taxa global de transferência de calor a partir das bolas para o ar ambiente.
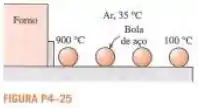
Passo 1
Dados fornecidos pelo enunciado:
Passo 2
Primeiro, começamos calculando o número de Biot para saber se podemos usar a análise de sistemas aglomerados. Podemos calcular Biot da seguinte maneira:
Aqui, é o coeficiente de transferência de calor por convecção, é a condutividade térmica da bola de aço e é o comprimento característico da bola de aço. Sabemos que o comprimento característico para esferas é
Aqui, é o diâmetro da bola de aço. Substituindo na ralação do número de Biot, temos:
Substituindo os valores fornecidos no enunciado temos:
O número de Biot é menos que , de modo que a análise do sistema aglomerado é aplicável.
Passo 3
Agora, podemos usar a equação da análise de sistemas aglomerado para encontrar o tempo de demora do processo de recozimento.
Calculamos primeiro a constante de tempo da seguinte maneira:
Substituindo o comprimento característico.
Aqui, é o coeficiente de transferência de calor, é a densidade e é a capacidade específica de calor a pressão constante.
Substituindo por , por , por e por , temos:
Passo 4
Podemos então calcular o tempo de demora do processo de recozimento da seguinte forma:
Podemos fazer umas mudanças nela da seguinte maneira:
Aqui, o tempo necessário para o resfriamento é , é constante Biot, é a temperatura ambiente, é a temperatura inicial e é a temperatura final.
Substituindo por , por , por e por na equação acima.
Portanto, o processo de recozimento ocorrerá em .
Passo 5
A taxa de transferência de calor para o ar ambiente de uma única bola pode ser expressa como:
Podemos calcular a massa de cada bola da seguinte maneira:
Assim, a transferência de calor de uma única bola é:
Temos então, que a taxa global de transferência de calor das bolas para o ar ambiente será:
Portanto, a taxa de transferência total das bolas para o ar ambiente é .