Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 20

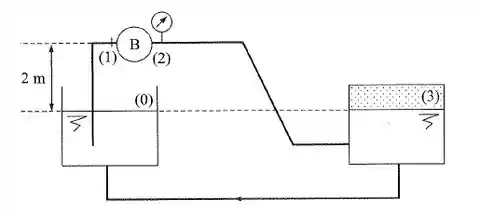
Na instalação da figura, os reservatórios são de pequenas dimensões, mas o nível mantém-se constante.

a) Qual é a vazão na tubulação que une a parte inferior dos dois tanques?

b) Para que aconteça essa vazão, qual a pressão em (3)?

c) Qual é a perda de carga na tubulação inferior dos dois tanques?

Dados: potência recebida pelo fluido da bomba N = 1,5   k W ; D 1 = 4   c m ; D 1 ≠ D 2 ; p 1 = 50   k P a   a b s ; p a t m = 100   k P a ; H p 0,1 = 2   m ; H p 2,3 = 4   m ; γ = 10 4   N / m 3 .

Passo 1

Vamos começar o exercício aplicando o equilíbrio de cargas entre os pontos 0 e 1:

H 0 = H 1 + H p 0,1

Abrindo a expressão:

v 0 2 2 g + p 0 γ + z 0 = v 1 2 2 g + p 1 γ + z 1 + H p 0,1

Isolando v 1 e substituindo os valores conhecidos:

v 1 2 2 g = v 0 2 2 g + p 0 γ + z 0 - p 1 γ - z 1 - H p 0,1

v 1 2 2 ( 10 ) = 0 2 2 10 + 100.10 3 10 4 + 0 - 50.10 3 10 4 - 2 - 2 → v 1 = 4,47   m / s

Agora podemos calcular a vazão através de:

Q = v 1 A 1 = v 1 π D 1 2 4 = 4,47 π 0,04 2 4 → Q = 5,62   m 3 / s

Passo 2

Agora vamos resolver a letra b). Vamos começar calculando a carga total exercida pela bomba através de:

N = γ Q H B → H B = N γ Q = 1,5.10 3 10 4 5,62.10 - 3 → H B = 26,7   m

Vamos começar aplicando o equilíbrio de cargas entre os pontos 1 e 3:

H 1 + H B = H 3 + H p 2,3

Abrindo a expressão:

v 1 2 2 g + p 1 γ + z 1 + H B = v 3 2 2 g + p 3 γ + z 3 + H p 2,3

Isolando p 3 e substituindo os valores conhecidos:

p 3 = γ v 1 2 2 g + p 1 γ + z 1 + H B - v 3 2 2 g + z 3 + H p 2,3

p 3 = 10 4 4,47 2 2 ( 10 ) + 50.10 3 10 4 + 2 + 26,7 - 0 2 2 ( 10 ) + 0 + 4 → p 3 = 307,2   k P a   ( a b s )

Com relação a pressão atmosférica, temos:

p 3 = p 3 a b s - p a t m = 307,2 - 100 → p 3 = 207,2   k P a

Passo 3

Agora, para resolver a letra c), vamos aplicar o equilíbrio de cargas entre os pontos 0 e 3:

H 3 = H 0 + H p 3,0

Abrindo a expressão, temos:

p 3 γ + v 3 2 2 g + z 3 = p 0 γ + v 0 2 2 g + z 0 + H p 3,0

Isolando H p 3,0 e susbtituindo os valores conhecidos:

H p 3,0 = p 3 γ + v 3 2 2 g + z 3 - p 0 γ + v 0 2 2 g + z 0

H p 3,0 = 307,2.10 3 10 4 + 0 2 2 ( 10 ) + 0 - 100.10 3 10 4 + 0 2 2 10 + 0 → H p 3,0 = 20,7   m

Resposta

Q = 5,62   m 3 / s

p 3 = 207,2   k P a

H p 3,0 = 20,7   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trabalhos de manutenção em sistemas hidráulicos de alta pressão exigem cuidados especiais. Um pequeno vazamento pode causar um jato de fluido hidráulico de alta velocidade que pode penetrar na pele e
O carrinho com pá defletora do Problema 4.128 se movimenta sem atrito. Ele deve acelerar para a direita. A velocidade do jato é V = 40m / s . A área do jato permanece constante em A = 25m m 2 . Descon
A água escoa em um duto circular. Em uma seção, o diâmetro é 0,3 m, a pressão estática é 260 kPa (manométrica), a velocidade é 3 m/s e a elevação é 10 m acima do nível do solo. Em uma seção a jusante,
Um túnel de vento de circuito aberto aspira ar da atmosfera através de um bocal com perfil aerodinâmico. Na seção de teste, onde o escoamento é retilíneo e aproximadamente uniforme, há uma tomada de p
Um jato de ar é soprado de um bocal perpendicularmente contra uma parede na qual existem duas tomadas de pressão. Um manômetro conectado à tomada colocada diretamente na frente do jato mostra uma altu