Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 19
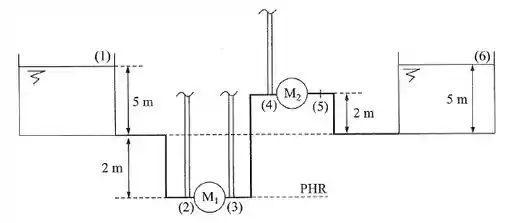
Na instalação da figura são dados:
Área da seção das tubulações:
Piezômetro (2):
Piezômetro (3):
Piezômetro (4):
Perda de carga no trecho (1)-(2) = 1,8 m e no trecho (5)-(6) = 2 m
; . Determinar:
a) o sentido do escoamento (justificar);
b) a vazão (L/s);
c) o tipo de máquina e sua potência;
d) o tipo de máquina e a potência trocada com o fluido.
Passo 1
Vamos começar o exercício encontrando as cargas totais nos pontos 3 e 4:
Agora, como o enunciado disse que a área da seção é constante, então a vazão e a velocidade são as mesmas para todos os pontos do sistema, dessa forma:
Como sabemos que o escoamento vai no sentido do ponto de maior carga para o de menor carga, então, como nesse caso , o escoamento vai de (6) para (1).
Passo 2
Agora vamos resolver a letra b). Para encontrar a vazão, precisamos da velocidade do fluido, para isso, vamos aplicar o equilíbrio de cargas entre os pontos 1 e 2:
Substituindo os valores conhecidos, temos:
Agora, a vazão será:
Passo 3
Agora, para a letra c), precisamos descobrir a variação de carga aplicada ao sistema pela máquina, se ela for negativa, é uma turbina, se for positiva, é uma bomba. Para isso, vamos aplicar o equilíbrio de cargas entre os pontos 2 e 3:
Abrindo a expressão, temos:
Isolando e substituindo os valores conhecidos, temos:
Como a carga é negativa, então temos uma turbina. Agora, para calcular a potência da turbina, podemos usar a seguinte equação:
Passo 4
Agora, para resolver a letra d), vamos aplicar o equilíbrio de cargas entre os pontos 4 e 6:
Abrindo a expressão, temos:
Isolando e susbtituindo os valores conhecidos:
Como a carga é positiva, então temos uma bomba. Agora, para calcular a potência que troca com o fluído, podemos usar a seguinte equação: