Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 72
Considere o sistema de escoamento mostrado no Problema 8.124. Considere que o mínimo NPSHR na entrada da bomba é 4,6 m de água. Selecione uma bomba apropriada para esta aplicação. Use os dados de aumento do fator de atrito com a idade do tubo do Problema 10.65 para estimar a redução de vazão após 10 anos de operação.
Passo 1
Beleza! Vamos começar o exercício aplicando o equilíbrio de energia para o sistema entre o ponto 1 indicado no enunciado e o topo do reservatório (ponto 2):
Como sabemos que no topo do reservatório temos , podemos considerar , então, a pressão obtida será manométrica. Sabemos também que podemos considerar a velocidade no reservatório igual a zero, então . E vamos considerar o nível do ponto 1 como referência, de maneira que , dessa forma a equação se torna:
E, sabemos que a perda de carga, contendo perdas distribuídas e localizadas, pode ser escrita como:
Como já temos a velocidade e o diâmetro da tubulação, vamos calcular a vazão do sistema, que será utilizada posteriormente para escolher uma bomba apropriada para as condições do problema:
Passo 2
Agora com a velocidade fornecida no enunciado, conseguimos encontrar o número de Reynolds, para isso, vamos pegar alguns dados da Tabela A.7 do livro:
Então, Reynolds será:
Agora, para encontrar o fator de atrito, precisamos primeiro pegar o dado referente à rugosidade da tubulação, que se encontra na tabela a seguir presente no capítulo 8:
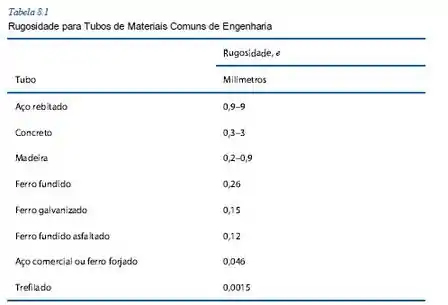
Então, como temos aço carbono, temos basicamente uma tubulação de aço comercial, então teremos . Então agora podemos usar a equação de Colebrook e descobrir o valor do fator de atrito:
Substituindo os valores conhecidos (lembrando que só conseguimos resolver essa equação com o auxílio de uma calculadora), temos:
Passo 3
Agora vamos voltar à equação do equilíbrio de energia do passo 1:
E substituir a expressão encontrada para a perda de carga no passo 1:
Agora precisamos recorrer às tabelas 8.2 e 8.4 apresentadas no livro e o diagrama para contração/expansão para encontrar os coeficientes de perda:
Nesse exercício, não temos nenhum acessório no sistema, então não teremos perda localizada referente à eles. Só teremos perda localizada na saída, devido à expansão brusca saindo da tubulação, então temos:
Passo 4
Agora que temos todos os dados, podemos substituir os valores conhecidos na equação de energia do passo 3, então:
Nesse caso, sabemos que o NPSHR fornecido no enunciado equivale a:
Então, substituindo os valores na equação de energia, temos:
Para essa altura de carga e para a vazão encontrada no passo 1, com o auxílio do diagrama de seleção de bombas a seguir:
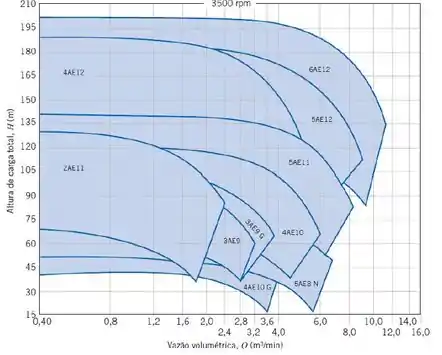
Não temos nenhuma bomba simples que atenda aos requisitos necessários, então precisamos recorrer a um diagrama com um sistema de bombas, mas os diagramas fornecidos no livro estão em unidades americanas, então precisamos converter a altura de carga e a vazão para poder encontrar uma bomba apropriada, então, temos:
Então, olhando o diagrama a seguir, temos:
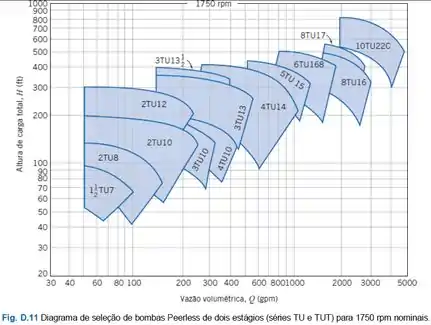
Podemos selecionar uma bomba 10TU22C de 2 estágios a 1750 rpm para atender aos requisitos do sistema.
Passo 5
Agora vamos verificar o caso para 10 anos, sabendo que o fator de atrito se relaciona com a idade da tubulação através de:
Então, o novo fator de atrito será:
Agora, vamos pegar a equação de energia encontrada no passo 4 e descobrir a nova velocidade com esse valor de atrito, já que manteremos a mesma carga para a bomba:
Substituindo os valores conhecidos, temos:
E, para essa velocidade, a nova vazão será: