Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas para exames de fundamentos de engenharia - Ex. 7

A bomba de um barco anti-incêndio fornece água para um bocal vertical com uma relação de diâmetro 3:1, como na Figura FE3.6. Se o atrito é desprezado e a bomba aumenta a pressão na seção 1 para 51 kPa (manométrica), qual será a vazão volumétrica resultante?

(a) 708 L/min, (b) 753 L/min, (c) 810 L/min, (d) 1.359 L/min, (e) 534 L/min

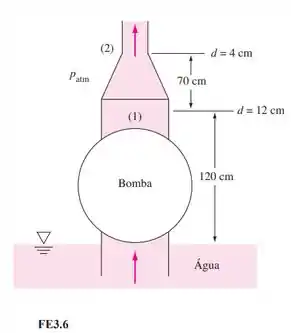
Passo 1

Vamos utilizar a equação de Bernoulli entre o ponto 1 e o ponto 2:

Vamos utilizar o ponto 1 como referencial para a altura, logo, . Como a pressão em 1 é a manométrica vamos utilizar a pressão atmosférica como zero.

Aplicando os dados em Bernoulli:

Uma relação entre e pode ser encontrada utilizando a equação da continuidade:

Logo:

A área da seção transversal do tubo em 2 é:

E a vazão pode ser encontrada por:

Resposta

Letra A) (a) 708 L/min

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como mencionado na Seção 4.10, o perfil de velocidade para escoamento laminar entre duas placas, como na Figura P4.41, é u = 4 u m á x y h - y h 2v = w = 0 á Se a temperatura em ambas as paredes é T p

Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?

Ar entra em um duto de L/D = 40 a V1 = 170 m/s e T1 = 300 K. O escoamento na saída está bloqueado. Qual é o fator de atrito médio no duto para escoamento adiabático?

Ar escoa adiabaticamente por um tubo de 2 cm de diâmetro. As condições na seção 2 são p 2 = 100k P a ,T 2 = 15 º CeV 2 =170m / s º . O fator de atrito médio é de 0,024. Na seção 1, 55 metros a montant

Ar entra em um tubo de 3 cm de diâmetro e 15 m de comprimento a V 1 =73m / s , p 1 =550k P a e T 1 =60 o C . O fator de atrito é 0,018. Calcule V 2,p 2 ,T 2ep 02 no final do tubo. Quanto de compriment