Enunciado
Operações Unitárias - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 35
Uma bomba centrífuga com rotor de 457 mm de diâmetro, girando a 880 rpm com água a 20 °C, gera os seguintes dados de desempenho:
Determine (a) o PMR, (b) o rendimento máximo e (c) a rotação específica. (d) Faça um gráfico da potência de eixo necessária em função da vazão.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma bomba centrífuga com diâmetro operando uma rotação de , bombeando água a ().O problema nos mostra também uma tabela com os dados de desempenho pra essa bomba.
O enunciado nos pede então pra determinar o ponto de máximo rendimento, o rendimento máximo , a rotação específica e também pra fazer um gráfico da potência de eixo em função da vazão .
Vem comigo pra gente matar esse problema juntos!
Passo 2
Pra começar a questão, vamos resolver as letras (a) e (b) e determinar o ponto de máximo rendimento e o rendimento máximo .
Primeiro, devemos vamos usar a tabela fornecida pelo enunciado converter os dados de de para e de de para .
Depois, vamos calcular os rendimentos pra cada uma das vazões, utilizando a Equação 11.5:
Realizando os cálculos pra cada um dos pontos a gente fica com a seguinte tabela:
Como a gente consegue ver na tabela acima, o maior valor de rendimento é no ponto onde a vazão volumétrica é .
Passo 3
Agora, vamos resolver a letra (c) e calcular a rotação específica adimensional a partir da Equação 11.30a (página 784):
Sendo e são a vazão e a altura de carga no ponto de projeto, o seja, no ponto de máximo rendimento.
Sendo assim:
Passo 4
Pra finalizar a questão, vamo resolver a letra (d).
Basta a gente construir um gráfico com a Potência em funlão da vazão a partir dos dados fornecidos na tabela que eu te mostrei no Passo 2:
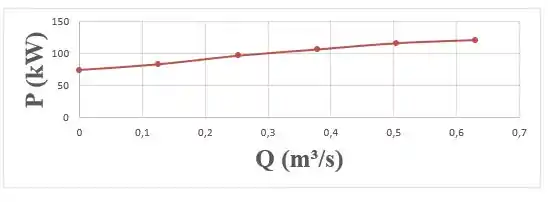
Pronto, matamos o problema juntos!
Resposta
(a) O PMR ocorre no ponto onde a vazão volumétrica é .
(b)
(c)
(d) O gráfico se encontra no Passo 4