Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Operações Unitárias - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 34

Foi pedido para você considerar uma bomba geometricamente semelhante a uma bomba Taco de 9 pol de diâmetro da Figura P11.34 para fornecer 75,7 l/s a 1.500 rpm. Determine os valores apropriados para (a) o diâmetro do rotor, (b) a potência no PMR, (c) a altura de carga com vazão nula e (d) o rendimento máximo. O fluido é querosene, em vez de água.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos uma bomba centrífuga com diâmetro do rotor D 1 = 9   p o l operando uma rotação de n 1 = 1760   r p m = 29,33   r p s , bombeando água a 20 ° C ( ρ 1 = 998   k g / m ³ ).

O enunciado nos pede então pra gente encontrar o diâmetro D 2 pra uma vazão de Q 2 = 75,7 L s = 0,0757 m 3 s a n 2 = 1500   r p m = 25   r p s . Além disso, devemos calcular a potência P no ponto de máximo rendimento, a altura de carga para uma vazão de Q = 0 e o rendimento máximo n 2 . Tudo isso pra querosene como fluido ( ρ 2 = 680   k g / m ³ ).

Vem comigo pra gente matar esse problema juntos!

Passo 2

Em primeiro lugar, vamos começar indo na figura e encontrando as propriedades no ponto de máximo rendimento:

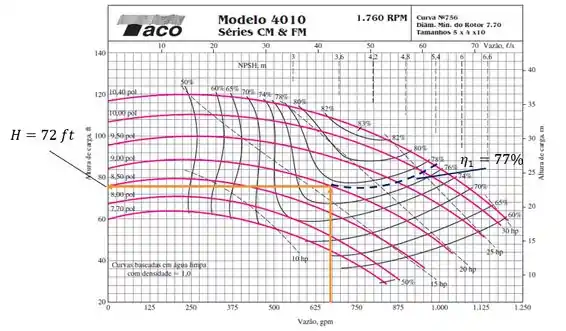
Como dá pra gente ver, o ponto de máximo rendimento pro diâmetro de D 1 = 9   p o l = 0,2286   m , a vazão é Q 1 = 675   g p m =   0,042     m 3 / s , altura de carga H 1 * = 72   f t = 21,95   m e o rendimento máximo η 1 = 77 % .

Passo 3

Agora, vamos resolver a letra (a) e calcular o diâmetro do rotor D 2 a partir da equação 11.28 (página 780):

Q 2 Q 1 = n 2 n 1 D 2 D 1 3

0,0757 m 3 s 0,042   m 3 s = 25   r p s 29,33   r p s D 2 0,2286   m 3

D 2 = 0,293   m = 11,5   p o l

Passo 4

Agora, vamos resolver a letra (c) e calcular a altura H 2 pra qual a vazão é nula.

Pra isso, basta ir de novo na figura com a curva de desempenho da bomba e calcular a altura pra qual a vazão é nula pra um diâmetro D 1 = 9   p o l . Encontraremos H 1 = 84   f t = 25,6   m .

Agora, só usar as leis de semelhança novamente pra calcular H 2 :

H 2 H 1 = n 2 n 1 2 D 2 D 1 2

H 2 25,6   m = 25   r p s 29,33   r p s 2 0,293   m 0,2286   m 2

H 2 = 30,55   m

Passo 5

Agora, vamos resolver a letra (d) e calcular o rendimento máximo η 2 .

Pra isso, vamos usar a correlação empírica de Moody, dada pela Equação 11,29a (página 781):

1 - η 2 1 - η 1 = D 1 D 2 1 / 4

1 - η 2 1 - 0,77 = 0,2286   m 0,293   m 1 / 4

η 2 = 0,784

Passo 6

Agora, vamos resolver a letra (b) e calcular a potência P no ponto de máximo rendimento.

Pra isso, primeiro, devemos calcular a altura de carga H 2 * nesse ponto, usando novamente a equação da lei de semelhança pra bombas:

H 2 * H 1 * = n 2 n 1 2 D 2 D 1 2

H 2 * 21,95   m = 25   r p s 29,33   r p s 2 0,293   m 0,2286   m 2 → H 2 * = 26,2   m

Agora podemos calcular a potência, usando H 2 * e a eficiência η 2 :

P = ρ 2 g Q 2 H 2 * η 2 = 680 k g m 3 9,81 m s 2 0,0757 m 3 s 26,2   m 0,784

P = 16,87   k W

Resposta

(a) D 2 = 11,5   p o l

(b) P = 16,87   k W

(c) H 2 = 30,55   m

(d) η 2 = 0,784

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bomba centrífuga da Figura P11.21 desenvolve uma vazão de 265 l/s de gasolina a 20 °C com um escoamento absoluto de entrada aproximadamente radial. Calcule para as condições teóricas (a) a potência,
Uma bomba centrífuga de 37 cm de diâmetro, operando a 2.140 rpm com água a 20 °C, produz os seguintes dados de desempenho:(a) Determine o ponto de máximo rendimento. (b) Faça um gráfico de CH em funçã
Suponha que o Problema P11.19 seja invertido para a condição de potência teórica Pw
Se a bomba de 38 pol de diâmetro da Figura 11.7b for utilizada para bombear querosene a 20 °C a 850 rpm e 1,39 m3/s, qual será (a) a altura de carga e (b) a potência de eixo resultantes?
Os dados do Problema P11.31 correspondem a uma rotação de 1.200 rpm da bomba. (Você conseguiria resolver o Problema P11.31 sem saber isso?) (a) Calcule o diâmetro do rotor. (Dica: Ver Problema P11.24.