Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 75
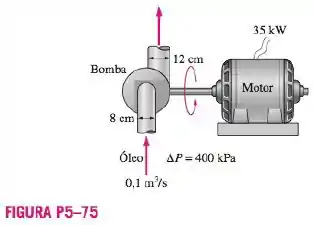
Uma bomba de óleo consome de energia elétrica enquanto bombeia óleo com a uma vazão de . Os diâmetros de entrada e saída do tubo são e , respectivamente. Se a elevação da pressão do óleo na bomba for medida como e a eficiência do motor for de , determine a eficiência mecânica da bomba. Considere o fator de correção da energia cinética como .
Passo 1
Temos a entrada da turbina, consideremos a entrada como , passando o óleo e temos que determinar a eficiência mecânica, adotaremos saída como (2).
Vamos assumir que o fluxo é constante e incompressível, como o enunciado nos deu eficiência do motor, temos que as perdas totais o nosso , pois, as perdas já estão contabilizadas na eficiência do motor. fator de correção teremos para todo o processo.
Para determinara a eficiência do motor, iremos executar o cociente da potencia útil pela potencial do motor.
Para determinar a eficiência temos que saber a carga útil da bomba utilizada, logo, escrevendo a equação do balanço de energia, temos:
Como nosso objetivo é determinar carga da turbina, vamos isola-la:
Perceba que falta, para determinar o resultado, as velocidades.
Passo 2
Vamos lá, precisamos determinar as velocidades.
Como o fluxo é conhecido de constante, e temos que para de terminar a velocidade basta dividir o fluxo pela área:
Repetindo o mesmo para :
Passo 3
Substituindo todos os cálculos feitos na equação da carga de turbina:
Passo 4
Para determinara a eficiência do motor, iremos executar o cociente da potencia útil pela potencial do motor.
Determinando a potencia útil:
Passo 5
Determinando a potencia da bomba de eixo:
Passo 6
Como digo anteriormente o cociente da potencia de útil pela de eixo nós resultaria na eficiência da motor, portanto: