Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 58

Uma bomba Peerles horizontal, de carcaça bipartida do tipo 4AE12, com rotor de diâmetro 280   m m , operando a 1750   r p m , eleva água entre dois reservatórios conectados por tubos de ferro fundido com 61   m de 100   m m e 61   m de 75   m m montados em série. A altura estática é de 3   m . Trace a curva de carga do sistema e determine o ponto de operação da bomba.

Passo 1

Considerações:

  1. Escoamento Estacionário;
  2. Fluído Incompressível;
  3. V 1 = V 2 = 0 (reservatório muito grande);
  4. p 1 = p 2 = p a t m ;
  5. K e n t r a d a = 0,5 ;
  6. K s a í d a = 1,0 .

Passo 2

Escreva a Equação de Bernoulli:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h t

Fazendo as considerações do Passo 1:

z 1 = z 2 + h t

H a = ∆ z + h t

Sendo:

h t = f L D ⋅ V 2 2 g + ∑ K V 2 2 g

Como não há perdas menores, temos que:

H a = ∆ z + ∑ f L D ⋅ V 2 2 g + ∑ K V 2 2 g

H a = ∆ z + f 1 L 1 D 1 ⋅ V 1 2 2 g + f 2 L 2 D 2 ⋅ V 2 2 2 g + 0,5 ⋅ V 1 2 2 g + 1 ⋅ V 2 2 2 g

Passo 3

Calculando V :

V = Q A = 4 Q π D 2

Sendo:

D 1 = 100   m m = 0,1   m ;

D 2 = 75   m m = 0,075   m .

Temos:

V 1 = 127 ⋅ Q

V 2 = 226 ⋅ Q

Passo 4

Do Número de Reynolds:

R e = ρ V D μ

Sendo:

μ = 1,01 x 10 - 3   N ⋅ s / m 2 (Tabela A.7);

ρ = 1000   k g / m 3 .

Temos:

R e 1 = 1000 ⋅ V 1 ⋅ 0 , 1 1,01 x 10 - 3 = 9,9 x 10 4 ⋅ V 1

R e 2 = 1000 ⋅ V 2 ⋅ 0 , 075 1,01 x 10 - 3 = 7,43 x 10 4 ⋅ V 2

Obtendo e D :

Com e tabelado para Ferro Fundido igual a 0 , 26   m m .

e D 1 = 2,6 x 10 - 4 0 , 1 = 0 , 0026

e D 1 = 2,6 x 10 - 4 0 , 075 = 0,00 35

Passo 5

Construa a seguinte tabela com valores para Q de 0 a 0,04   m 3 / s

Com o Diagrama de Moody, obteremos os valores para f .

Com a Equação do Passo 2, calcularemos H a .

Com a Figura D.4, obtemos os valores de Q e H a para uma bomba Peerles horizontal, de carcaça bipartida do tipo 4AE12, com rotor de diâmetro 280   m m , operando a 1750   r p m .

Convertendo m 3 / m i n para m 3 / s .

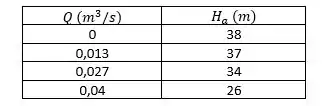
Passo 6

Traçando a curva de carga do sistema e determinando o ponto de operação da bomba.

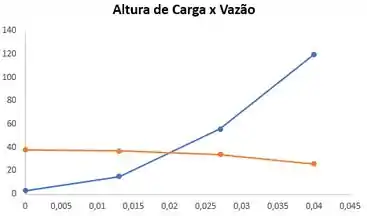
O ponto de operação da bomba é o ponto que as curvas se interceptam.

Esse ponto acontece quando Q = 0,02   m 3 / s e H a = 33   m .

Resposta

Q = 0,02   m 3 / s

H a = 33   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 10.37 apresenta dados para a eficiência de uma grande roda de água Pelton instalada na Usina Hidrelétrica de Tiger Creek da Pacific GasEletric Company, perto de Jackson, na Califórnia. Esta u
Em unidades típicas dos Estados Unidos, a definição comum de velocidade específica para uma turbina hidráulica é dada pela Eq. 10.13b. Desenvolva uma conversão entre essa definição e outra verdadeiram
Uma turbina de impulsão sob uma altura de carga líquida de 9,9 m foi testada para diferentes velocidades. As vazões e as forças de frenagem para a série de velocidade foram registradas:Calcule e faça
Uma turbina de impulsão deve desenvolver 15 MW com roda única, em um local onde a altura de carga líquida é 350 m. Determine a velocidade, o diâmetro do rotor e o diâmetro do jato apropriado para oper
A hélice de um barco de propulsão a ar, usado no parque nacional de Everglades, na Flórida, movimenta ar à taxa de 50 kg/s. Quando em repouso, a velocidade da corrente de ar atrás da hélice é de 45 m/