Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 57
Parte do suprimento de água para o Setor Sul do Parque Nacional do Grand Canyon é oriunda do Rio Colorado [54]. Uma vazão de , tomada do rio a uma elevação de , é bombeada para um tanque de armazenagem acima do Setor Sul, na elevação de . Parte da tubulação está acima do solo e parte em uma galeria perfurada direccionalmente em ângulos de até a partir da vertical; o comprimento total da linha é de . Sob condições de operação em regime permanente, a perda de carga por atrito é de de água em adição à altura estática. Estime o diâmetro do tubo de aço comercial do sistema. Calcule a potência de bombeamento requerida, se a eficiência da bomba for .
Passo 1
Considerações:
- Escoamento Estacionário;
- Fluído Incompressível;
- (reservatório muito grande);
- .
Passo 2
Escreva a Equação de Bernoulli:
Fazendo as considerações do Passo 1:
Sendo:
Como não há perdas menores, temos que:
Passo 3
Como não possuímos o tamanho do diâmetro, devemos fazer um chute inicial e uma sequência de iterações até um valor convergente.
Chute Inicial
Calculando :
Sendo:
;
.
Temos:
Passo 4
Do Número de Reynolds:
Sendo:
(Tabela A.7);
.
Temos:
Obtendo :
Com tabelado para Aço Comercial igual a .
Com o Diagrama de Moody, obtemos os seguintes valores para :
Passo 5
Sob condições de operação em regime permanente, a perda de carga por atrito é de de água em adição à altura estática.
Então, o diâmetro iterado deve nos proporcionar .
Voltando na equação de :
Sendo:
;
;
Temos:
Repetiremos os Passos 3, 4 e 5 para diferentes valores de diâmetros:
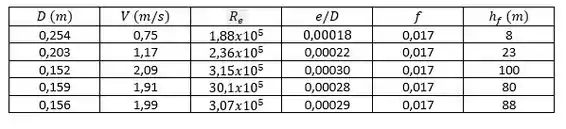
Assim, temos que o diâmetro é igual a .
Passo 6
Voltando na Equação do Passo 2:
Sendo:
.
Temos:
Passo 7
Calculando a potência da bomba.
Temos uma eficiência de .
Então: