Bombas de calor, com base no subsolo, operam usando o solo, em vez do ar ambiente, como a fonte de calor (ou sumidouro) para aquecimento (ou resfriamento) de construções. Um líquido troca energia com o solo (recebendo ou doando) através de uma tubulação plástica que é enterrada. A tubulação encontra-se em uma profundidade na qual as variações anuais na temperatura do solo são muito menores daquelas no ar ambiente. Por exemplo, em um local como South Bend, Indiana, a temperatura no subsolo a certa profundidade pode se manter em aproximadamente enquanto as variações, ao logo do ano, da temperatura do ar ambiente têm uma faixa de a . Suponha que a tubulação esteja disposta em um arranjo em serpentina com pequeno espaçamento.

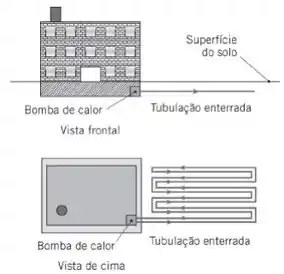
Em qual profundidade a tubulação deve ser enterrada de modo que o solo seja visto como um meio infinito a temperatura constante em um período de meses? Leve em conta o resfriamento (aquecimento) periódico do solo em função das variações anuais nas condições ambientais e das mudanças na operação da bomba de calor do modo aquecimento no inverno para o modo resfriamento no verão.

Para resolver essa questão vamos assumir que:

(1) As condições são periódicas;

(2) As propriedades são constantes;

(3) A transferência de calor é unidimensional (tubulação com espaçamento estreito);

(4) A variação diurna da temperatura ambiente é pequena em relação à sua variação anual.

Como o aquecimento e o resfriamento do solo estão associados a mudanças anuais nas temperaturas ambiente e soterramento da tubulação, a profundidade do enterro, , deve ser maior que o dobro da profundidade de penetração associada ao aquecimento periódico do solo. Ou,

A frequência de aquecimento é:

Então, a profundidade de enterro necessária, considerando que as propriedades do solo foram pegas na Tabela A.3, é: