Um fio elétrico de de diâmetro é isolado por uma bainha emborrachada de de espessura , e a interface fio/bainha é caracterizada por uma resistência de contato térmico de . O coeficiente de transferência de calor por convecção na superfície externa da bainha é de e a temperatura do ar ambiente é de . Se a temperatura do isolamento não pode exceder , qual é a potência elétrica máxima permitida que pode ser dissipada por unidade de comprimento do condutor? Qual é o raio crítico do isolamento?
Passo 1
Fala galerinha!! Vocês estão bem??
Para resolver essa questão, podemos começar fazendo as seguintes suposições:
(1) Estado estacionário.
(2) Condução radial unidimensional através do isolamento.
(3) Propriedades constantes.
(4) Troca de radiação insignificante com o ambiente.
Os dados fornecidos foram:
Diâmetro do fio:
Espessura do isolante:
Raio interno:
Raio externo:
Coeficiente convectivo na superfície:
Condutividade térmica do isolante:
Resistência de contato fio/bainha:
Temperatura do ar ambiente e grandes arredores:
Temperatura máxima do isolante:
Passo 2
Para resolver essa questão, podemos fazer um circuito térmico que representa a condução de calor no sistema. O circuito tem a seguinte forma:
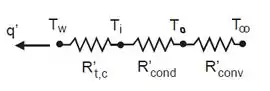
A temperatura máxima de isolamento corresponde à sua superfície interna e é independente da resistência de contato. Do circuito térmico, podemos escrever o seguinte:
Substituindo os termos da expressão acima pelos dados fornecidos, temos:
Portanto, a potência máxima é .
Passo 3
O raio de isolamento crítico também não é afetado pela resistência de contato, portanto, ele é dado por:
Portanto, o raio crítico é .