Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 89

Calcule o valor do fator de forma H para o caso limite de uma camada limite que é infinitesimalmente fina (Figura P 10 - 89 ). Esse valor de H é o valor mínimo possível.

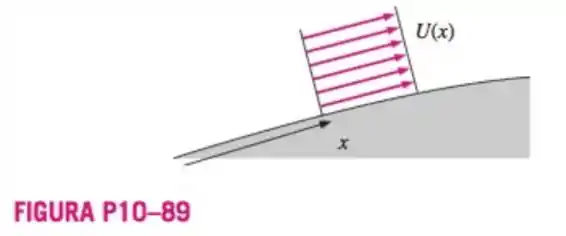
Passo 1

Lembra que o fator de forma é calculado por:

H = δ * θ

Então e se fizermos pela definição de espessura de deslocamento e da espessura da quantidade de movimento que é:

δ * = ∫ 0 ∞ 1 - u U d y

θ = ∫ 0 ∞ u U 1 - u U d y

Então:

H = ∫ 0 ∞ 1 - u U d y ∫ 0 ∞ u U 1 - u U d y

Aí é aqui nos momentos de dificuldade que precisamos pensar muito bem o que estamos fazendo e realmente entender o que é isso tudo na nossa frente (Responde Aí, o coach).

Como o enunciado nos disse que a camada limite é infinitesimalmente fina então isso nos induz em pensar que δ * = 0 e θ = 0 , o que nos leva há uma indeterminação em relação ao fator de forma ou seja H = 0 0 , e também por ser incrivelmente fina essa placa podemos dizer que a relação u U → 1 , pois a velocidade u junto a placa tende a não se afetar com isso. Então vamos fazer u → U :

H = lim u → U ⁡ ∫ 0 ∞ 1 - u U d y ∫ 0 ∞ u U 1 - u U d y

Passo 2

Só que não adianta muito o que a gente faça em relação a essa equação, nada parece adiantar muito né? Temos que forçar alguma coisa em cima e embaixo da nossa equação pra que possamos avançar na nossa análise, bem já que estamos integrando em cima e em baixo, por que não derivar?

Hmm... pode ser mas pelo que? Por u mesmo, afinal ele está em todos os numeradores e derivada de numerador é mais fácil, então podemos escrever a derivada da seguinte forma:

H = lim u → U ⁡ d d u ∫ 0 ∞ 1 - u U d y d d u ∫ 0 ∞ u U 1 - u U d y = lim u → U ⁡ ∫ 0 ∞ d d u 1 - u U d y ∫ 0 ∞ d d u u U 1 - u U d y

Escrever a integral ou a derivada primeiro não faz muita diferença, então fazendo a derivada teremos:

H = lim u → U ⁡ ∫ 0 ∞ - 1 U d y ∫ 0 ∞ d d u u U - u 2 U 2 d y

H = lim u → U ⁡ ∫ 0 ∞ - 1 U d y ∫ 0 ∞ 1 U - 2 u U 2 d y

Melhorando um pouco a aparência da parte de baixo nós temos:

H = lim u → U ⁡ ∫ 0 ∞ - 1 U d y 1 U ∫ 0 ∞ 1 - 2 u U d y

Jogando 1 / U que está no denominador pro numerador nós teremos:

H = lim u → U ⁡ - ∫ 0 ∞ d y ∫ 0 ∞ 1 - 2 u U d y

Agora aplicando o limite temos:

H = - ∫ 0 ∞ d y ∫ 0 ∞ 1 - 2 U U d y = - ∫ 0 ∞ d y ∫ 0 ∞ 1 - 2 d y = - ∫ 0 ∞ d y - ∫ 0 ∞ d y = 1

E esse é o menor valor possível para H , e todos os valores do fator de forma obrigatoriamente serão maiores que 1, e esse valor se dá para um regime muito turbulento. Onde a placa nem faz nenhuma diferença ali.

Resposta

H = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. Um campo de escoamento é simulado por um programa de Dinâmica dos Fluidos Computacional que usa a pressão modificada em seus cálculos. Na Figura P10-14 está um perfil da pressão modificada ao long
11. Considere o escoamento Poiseuille planar do Problema 10-10. Discuta como a pressão modificada varia com a distancia x a jusante. Em outras palavras, a pressão modificada aumenta, permanece a mesma
13. Escreva as três componentes da equação de Navier-Stokes em coordenadas cartesianas em termos da pressão modificada. Insira a definição de pressão modificada e mostre que as componentes x, y e z sã
8. Qual é o parâmetro adimensional na equação de Navier-Stokes na forma admensional que é eliminado pelo uso da pressão modificada em lugar da pressão verdadeira? Explique.
15. No exemplo 9-18 resolvemos a equação de Navier-Stokes para escoamento laminar permanente, completamente desenvolvido em um tubo redondo (escoamento de Poiseuille), desprezando a influencia da grav