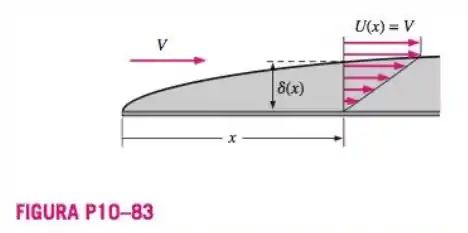
A componente da velocidade na corrente de uma camada limite sobre placa plana permanente, incompressível, laminar e de espessura é aproximada pela expressão linear simples, para e para (Figura ). Gere expressões para espessura de deslocamento e espessura do momento em função de , baseado nessa aproximação linear. Compare os valores aproximados de e com os valores de e obtidos na solução de Blasius.

Respostas: 0.500, 0.167

Já na página (da primeira edição do livro em português) temos a definição da espessura do momento ,que concordo que é uma letra horrível para isso, que é dada por:

Então aplicando a aproximação para :

Fazendo essa integral temos:

Fazendo o intervalo:

Então:

Note que não nos interessa a condição para quando , pois estaremos fora da camada limite e a velocidade não se altera por isso, não tendo porque ter uma análise.

Agora vamos ver se essa aproximação foi boa, sabendo que a medida real da espessura do momento e a espessura do deslocamento são:

Seguindo o exemplo 10-10 da primeira edição desse livro (onde ele assume , poderíamos supor qualquer relação, uma vez que encontraremos um relação entre o real e o teórico em qualquer posição dessa placa)nós temos que pela tabela de Blasius que:

Portanto dividindo uma pela outra temos:

Fazendo o mesmo raciocínio para a espessura do momento:

Então o erro causado será de:

O que são erros bem grandes para , portanto a aproximação é ruim.