Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 22

Uma camada de líquido separa duas superfícies planas, conforme mostrado. A superfície inferior é estacionária; a superfície superior move-se para baixo com velocidade constante, V. A superfície móvel tem largura, w, perpendicular ao plano da figura e w ≫ L. A camada de líquido incompressível, de massa específica ρ, é espremida para fora do espaço entre as superfícies. Considere que o escoamento é uniforme em qualquer seção e despreze a viscosidade como primeira aproximação. Use um volume de controle adequadamente escolhido para mostrar que u = Vx/b dentro da fresta, em que b = b0 - Vt. Obtenha uma expressão algébrica para a aceleração de uma partícula fluida localizada em x. Determine o gradiente de pressão, ∂p/∂x, na camada líquida. Determine a distribuição de pressão, p(x). Obtenha uma expressão para a força resultante de pressão que age sobre a superfície (móvel) plana superior.

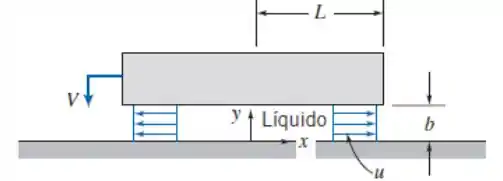
Passo 1

Pessoal, vamos primeiro provar que u = V   x / b . Para isto iremos aplicar a equação da conservação de massa:

0 = ∂ ∂ t ∫ ρ d V +   ∫ ρ V → d A →

Como o liquido esta sendo espremido e saindo pelas laterais, haverá variação de massa no sistema. Uma vez que as placas são planas e considerando uma variação infinitesimal na altura, a equação será reduzida para:

0 = ∂ ∂ t ∫ 0 y ρ w x d y +   ∫ 0 y ρ u w d y

0 = ρ w x d y d t +   ρ u w y

Podemos observar pela figura que a variação de altura pela placa superior em função do tempo é –V. d y d t = - V

Substituindo:

0 = ρ w x ( - V ) +   ρ u w y

u = x y V

Outra maneira:

Além disso, temos uma relação entre V e u, pois o volume deslocado na vertical é o mesmo que escoará pela horizontal. Veja o desenho:

V o l u m e   a n t e s = V o l u m e   d e p o i s

w x d y = w y d x

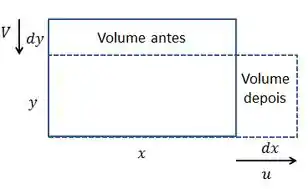
Derivando em função do tempo:

x d y d t = y d x d t

x V = y u

u = x y V

Usando o referencial do enunciado b = b 0 - V t , que é o inverso de y (em t=0, y = b 0 ).

u = x b V

Passo 2

A equação da aceleração da partícula em x é dada pela equação:

a x = D u D t = u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z + ∂ u ∂ t

Simplificando a expressão, ficamos com:

a x = u ∂ u ∂ x + ∂ u ∂ t

a x = x b V ∂ x b V ∂ x + ∂ u ∂ b ∂ b ∂ t

a x = x b V ∂ x b V ∂ x + ∂ x b V ∂ b ∂ b 0 - V t ∂ t

a x = x b 2 V 2 + - x V b 2 ( - V )  

a x = 2 x b 2 V 2

Passo 3

Para encontrar o gradiente de pressão, vamos usar a equação de Euler em x:

ρ a x = ρ g x - ∂ p ∂ x

Substituindo a x e sendo g x = 0 :

ρ 2 x b 2 V 2 = - ∂ p ∂ x

∂ p ∂ x = - 2 ρ V 2 b 2 x

Passo 4

A distribuição de pressão pode ser encontrada integrando a equação do gradiente:

d p d x = - 2 ρ V 2 b 2 x

p = - 2 ρ V 2 b 2 ∫ L x x d x

p = - ρ V 2 b 2 x 2 - L 2

p = ρ V 2 L 2 b 2 1 - x L 2

Passo 5

A equação geral da força é dada por:

F = ∫ p d A

Substituindo o valor de p, da área onde a força atua ( d A = w d x ) e usando o intervalo de 0 a L, temos (Atenção que no comprimento total temos 2L):

F y = 2 ∫ 0 L ρ V 2 L 2 b 2 1 - x L 2 w d x

F y = 2 ρ w V 2 L 2 b 2 x - 1 3 x 3 L 2  

F y = 2 ρ w V 2 L 2 b 2 L - 1 3 L  

F y = 4 3 ρ w V 2 L 3 b 2

Resposta

a x = 2 x b 2 V 2          

∂ p ∂ x = - 2 ρ V 2 b 2 x

p = ρ V 2 L 2 b 2 1 - x L 2

F y = 4 3 ρ w V 2 L 3 b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.51 Após uma chuva, a concentração de sedimentos em um certo ponto de um rio aumenta à taxa de 100 partes por milhão (ppm) por hora. Além disso, a centração de sedimentos aumenta com a distância rio
A componente x da velocidade em um campo de escoamento bidimensional e incompressível é dada por u = A x 2 ; A = 3,28m - 1 . s - 1 e as coordenadas são medidas em metros, Não há componente ou variação
A componente x da velocidade em um campo de escoamento bidimensional, incompressível, é dada por u = A x y , as coordenadas são medidas em metros e A = 2m - 1 . s - 1 . Não há componente ou variação d
O campo de velocidade, para uma fonte plana localizada a uma distância h = 1m acima de uma parede infinita alinhada ao longo do eixo x , é dado por: V → = q 2 π x 2 + y - h 2 x i → + y - h j → + q 2 π
5.87 O perfil de velocidade para o escoamento inteiramente desenvolvido em um tubo circular é V r = V m á x 1 - r R 2 á . Avalie as taxas de deformação linear e angular para este escoamento. Obtenha u