Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 37

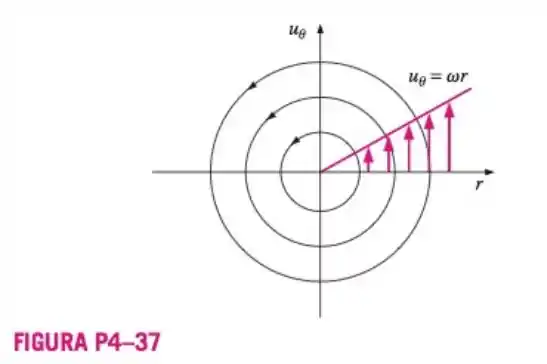
O campo da velocidade para a rotação de corpo rígido no plano r θ (Figura P 4 - 37 ) é dado por

u r = 0       u θ = ω r

Onde ω é o módulo da velocidade angular ( ω → aponta para a direção z). No caso com ω = 1.0   s - 1 , trace o gráfico de contorno do módulo de velocidade (velocidade escalar). Especificamente, desenhe curvas de velocidade constante V = 0.5 ,   1.0 ,   1.5 ,   2.0 e 2.5   m / s . Verifique se essas velocidades estão rotuladas em seu esboço. Certifique-se de identificar estas velocidades escalares no seu gráfico.

Passo 1

Como não temos velocidade radial (ou seja o corpo não gira em torno de si mesmo) então a função velocidade pode ser escrita como:

V = ω r

Se tivesse uma velocidade radial poderíamos calcular a velocidade total como:

V = u θ 2 + u r 2

Isso vem por que temos uma posição que respeita a equação de um círculo, então a equação das velocidades respeita a lei de Pitágoras.

E como ω = 1 , logo:

V = r

Então quando V = 0.5 → r = 0.5 , V = 1 → r = 1 e por aí vai, nos dando o seguinte gráfico:

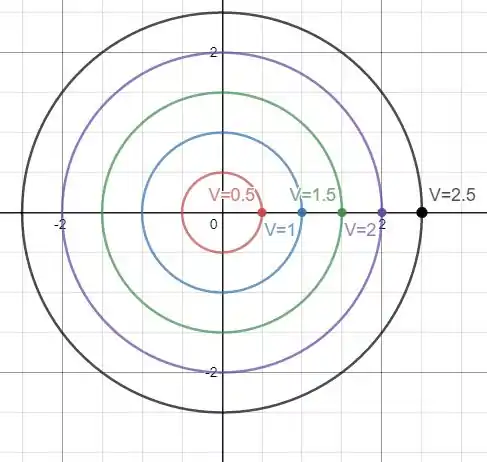
A velocidade é constante para cada um desses círculos.

Resposta

Imagem do passo 1.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.
Combine seus resultados do Problema 4 - 88 para formar o tensor taxa de deformação simétrico ϵ y . ϵ i j = ϵ r r ϵ r x ϵ x r ϵ x x Os eixos x e r são principais?
Considere o escoamento de Poiseuille bidimensional do problema 4-79. O fluido entre as placas é água a 40 ° C . Seja h = 1,6 m m a altura da lacuna e d P d x = - 230 N / m 3 o gradiente de pressão. Ca
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Use a taxa de deformação volumétrica para verificar se esse campo de escoame