Se o carrinho do Problema 4.138 inicia o movimento em , em que instante você esperaria a aceleração máxima? Esboce a sua expectativa para a curva de aceleração em função do tempo. Qual o valor de que daria a máxima aceleração em qualquer instante? Por que? A velocidade do carrinho poderá em algum instante igualar-se à velocidade do jato? Explique de forma sucinta.

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

Como estamos analisando um sistema , temos:

Não há forças de campo atuando no sistema, então, :

Não temos a variação das propriedades com o tempo, então:

Assim:

Sendo que:

Então:

Para o fluxo de entrada, possuem uma inclinação de 180°, então .

Aqui, indica a velocidade relativa do fluxo de entrada, já , a velocidade relativa do fluxo de saída para as mesmas condições.

;

.

Então:

A partir da equação obtida percebemos que a aceleração é máxima é em , já que nesse tempo a velocidade do carrinho é igual a 0, e consequentemente a resistência será nula.

Esboçando a sua expectativa para a curva de aceleração em função do tempo, temos uma diminuição resultante do quadrado da aceleração obtida pelo carrinho:

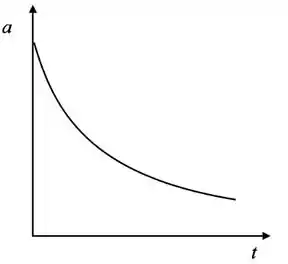
O valor de que daria a máxima aceleração em qualquer instante é de 90°, isso porque nesse ângulo o momento atua totalmente na direção vertical, sendo .

Para sabermos se a velocidade do carrinho poderá em algum instante igualar-se à velocidade do jato, devemos substituir por :

Percebemos que obtivemos uma aceleração negativa, assim, temos que a velocidade do carrinho não poderá igualar-se à velocidade do jato por conta da resistência contraria ao movimento do carrinho.