Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 26
Apóia-se um peso sobre um pistão de de diâmetro, e a leitura do manômetro da figura é . A viscosidade do fluido é e o comprimento do pistão é . Adotando o modelo de duas placas planas paralelas, determinar a folga entre o pistão e o cilindro para que o pistão desça apenas por minuto. Adotar uma queda de pressão linear ao longo do escoamento na folga.
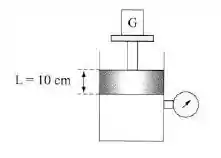
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para encontrar a folga entre o pistão e o cilindro para as condições pré-determinadas, temos que:
Onde:
Portanto:
Resposta
Exercícios de Livros Relacionados
A componente y da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é v = A x y ( x 2 - y 2 ) , em que A = 3m - 3 ⋅ s - 1 e x ey são medidos em metros. Determi
A componente x da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é u = A / x , em que A = 2m 2 / s e x é medido em metros. Determine a mais simples componen
A componente x da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é u = A e x / bcos ( y / b ) , em que A = 10m / s e b = 5m e x e y são medidos em metros.
A componente x da velocidade em um campo de escoamento em regime permanente e incompressível no plano x y é v = 2 x y x 2 + y 2 2 Mostre que a expressão mais simples para a componente x da velocidade
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação senoidal de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U , na