Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 82

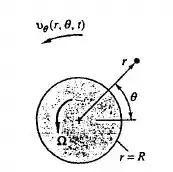
Um cilindro circular sólido de raio R gira a uma velocidade angular Ω em um fluido viscoso incompressível que está em repouso distante do cilindro, como mostra a figura abaixo. Adote hipóteses simplificadoras e deduza a equação diferencial governamental e as condições de contorno para o campo de velocidade v θ no fluido. Não resolva a mesma que você esteja obsecado por este problema. Qual é o campo de escoamento permanente para este problema?

Passo 1

E aí, gente!!! Tranquilo? Vamos encarar mais um problema de mecânica dos fluidos com as equações de Navier Stokes?

Bem, o enunciado nos diz que a única componente da velocidade que é importante é a angular, ou seja, apenas a componente que depende do ângulo, em outras palavras v θ . Isso quer dizer que precisamos focar apenas na equação da componente dita, show?

Passo 2

As nossas simplificações feitas de acordo com o enunciado dizem que v z = v r = 0 e que as propriedades não variam com o ângulo, de forma matemática, ∂ ∂ θ = 0 .

Simplificando assim, a nossa equação de Navier-Stokes toma a seguinte forma:

∂ v θ ∂ t = μ ρ 1 r ∂ ∂ r r ∂ v θ ∂ r - v θ r 2

Passo 3

Quais são as condições de contorno desse problema? Bem a gente sabe que nas exterminadas do nosso cilindro, a velocidade ali será exatamente a velocidade de rotação, ou seja,

v θ R ,   t = Ω R

E muito, mas muito longe do cilindro temos que não há nem sequer a influência dessa velocidade de rotação, certo? Então podemos dizer que quando R infinito, temos que a velocidade será zero!

v θ ∞ , t = 0

Resposta

∂ v θ ∂ t = μ ρ 1 r ∂ ∂ r r ∂ v θ ∂ r - v θ r 2

v θ R ,   t = Ω R

v θ ∞ , t = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Uma partícula de fluido (A) está localizada no eixo x = x A no instante t =
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Uma partícula de fluido (A) está localizada no eixo x = x A e y = y A no ins
Considere o campo de velocidade em regime permanente incompressível e bidimensional do Problema 4 - 33 . Gere um gráfico vetorial do campo de aceleração no quadrante superior direito de x = 0a5 e de y
O campo da velocidade para uma linha de vórtices no plano r θ (Figura P 4 - 38 ) é dado por u r = 0u θ = K r Onde K é a intensidade da linha de vórtices. No caso com K = 1.0m / s 2 faça o gráfico de c
O campo da velocidade para a rotação de corpo rígido no plano r θ (Figura P 4 - 37 ) é dado por u r = 0u θ = ω r Onde ω é o módulo da velocidade angular ( ω → aponta para a direção z). No caso com ω =