Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 45

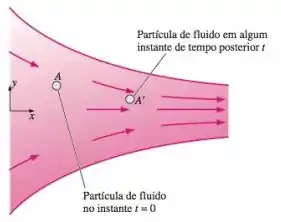
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Uma partícula de fluido (A) está localizada no eixo e no instante (Figura P4-45). Em algum instante posterior , a partícula de fluido moveu-se a jusante com o escoamento até algum novo local , , como mostra a figura. Gere uma expressão analítica para a localização da partícula de fluido em qualquer instante arbitrário em termos de sua posição inicial e das constantes . Em outras palavras, deduza uma expressão para . (Sugestão: Sabemos que seguindo uma partícula de fluido. Substitua , separe as variáveis e integre.)

Passo 1

Vamos começar com as hipóteses do problema:

O escoamento está em regime permanente;
O escoamento é bidimensional no plano

Vamos relembrar que o nosso campo de velocidade é descrito por:

Passo 2

Vamos começar a dedução pela definição da componente velocidade :

com condição inicial , . Rearranjando e separando as variáveis temos:

Integrando ambos os lados temos:

Podemos definir , por conveniência, e assim temos:

Como , temos que:

Passo 3

Aplicando as condições iniciais definidas para o modelo diferencial temos:

Logo, para a posição da partícula em um tempo arbitrário () temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verdadeiro ou falso: para cada afirmação, decida se ela é verdadeira ou falsa e discuta rapidamente sua resposta. (a)O teorema de transporte de Reynolds é útil para transformar as equações de conserva

Considere o escoamento de Couette — o escoamento entre duas placas paralelas infinitas separadas pela distância h , com a placa superior se movendo e a placa inferior fixa, como ilustra a Figura P 7 -

Considere a forma geral do teorema de transporte de Reynolds (TTR) dada por d B s i s t d t = d d t ∫ ρ b d V + ∫ ρ bV r → ∙ n → d A onde V r → é a velocidade do fluido com relação à superfície de con

Combine seus resultados do Problema 4 - 72 para formar o tensor de taxa de deformação bidimensional ε i j . ε i j = ε x x ε x y ε y x ε y y Os eixos x e y são principais?

Para o escoamento de Couette da Figura P 4 - 71 , calcule as taxas de deformação linear nas direções x e y , e calcule a taxa de deformação por cisalhamento ε x y .