Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 9
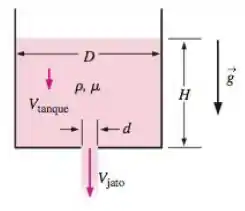
9. Considere o escoamento da água através de um pequeno furo no fundo de um grande tanque cilíndrico (Figura P10-9). O escoamento é laminar em todos os pontos. O diâmetro d do jato é muito menos do que o diâmtro D do tanque, mas D é da mesma ordem de grandeza da altura H do tanque. Carrie que ela pode usar a aproximação de estática dos fluidos em todos os pontos no tanque exceto perto do furo, mas ela quer confirmar essa aproximação matematicamente. Ela considera a velocidade característica no tanque como . O comprimento característico é a altura H do tanque, o temo característico é o tempo necessário para drenar o tanque e a diferença de pressão de referencia é (diferença de pressão entre a superfície da água e o fundo do tanque, usando a estática dos fluidos). Substitua todos esses valores de escala na equação ne Navier-Stokes na forma adimensional incompressível ( Equação 10-6) e verifique por uma análise de orgem de grandeza que para , só permanecem os termos de pressão e gravidade. Em particular, compare a ordem de grandeza de cada termo com cada um dos quatro parâmetros admensionais St, Eu, Fr e Re. (Sugestão: ). Sob qual critério, a aproximação de Carrie é adequada?
Passo 1
E ai, tudo certo?
Neste caso estamos diante de um enunciado gigante, porém não se assuste com isso. Basta ler o mesmo com calma e observar na equação em que ele manda substituir os valores a serem encontrados. Além de substituir, devemos lembrar que cada parâmetro admensional tem sua definição detalhada ao longo do capítulo e durante a resolução da questão.
Então, vem comigo!
Sabemos que a equação não dimensional de Navier-Stokes é,
O número Strouhal é dado como,
Aqui a frequência pode ser escrita como inversa do tempo característico.
Agora, a equação de St se torna.
Agora é,
Portanto, a equação acima se torna,
Portanto,
Portanto, a ordem de magnitude de é 1.
Passo 2
O número de Euler é,
Aqui a diferença de pressão pode ser escrita como como indica o enunciado.
A equação acima torna-se,
Nós sabemos também do enunciado que,
A equação acima se torna,
De acordo com a conservação da massa,
Portanto,
Portanto, a equação de Euler se torna,
Portanto, .
Vem comigo, estamos quase lá!!!
Passo 3
O número de Froude é,
É dado pelo enunciado que,
A equação torna-se,
De acordo com a conservação da massa,
Portanto,
Portanto, o número de Froude é, .
Agora, o número de Reynolds, aquela equaçãozinha clássica
Aqui,
A equação torna-se,
Note que acima multiplicamos e dividimos pela .
De acordo com a conservação da massa,
Portanto,
Agora, a equação do Re se torna,
Portanto, o número de Reynolds é,
Agora, a equação a equação não dimensional de Navier-Stokes é,
Na equação acima, os valores aproximados dos termos são,
Para nos dois primeiros, os termos são insignificantes em comparação com outros termos.
Para o último termo, que é o termo viscoso, selecione o escoamento para laminar, é da ordem de .
Assim, para que o termo viscoso seja da mesma ordem de grandeza do termo inercial, d 2 / D 2 , ele precisa ser da ordem de!
Nossa resposta, dessa forma, será a equação de Navier-Stokes para fluidos em repouso:
Show, conseguimos terminar!!
Resposta
Verificação em texto