Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 55

Gate AB in Fig. P2.55 is 5 ft wide into the paper, hinged at

A, and restrained by a stop at B. The water is at 208C.

Compute (a) the force on stop B and (b) the reactions at A

if the water depth h 5 9.5 ft.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Considerando a geometria do portão

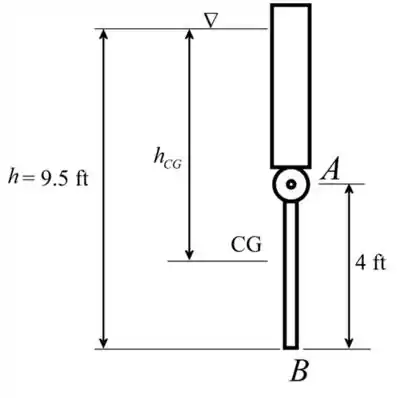
Aqui, é a posição de centroide C G e é a posição de centroide a h C G partir do dado.

Passo 2

Encontre a localização do centroide a partir do dado.

h C G   = ( h - 4 ) + 4 2   = ( 9.5 - 4 ) + 2   = 7.5 f t

Calcule a área da seção transversal do portão retangular.

A   = 5 × 4   = 20 f t 2

Passo 3

Calcule a força hidrostática total no portão usando a seguinte relação:

F = γ á gua   A h C G

Aqui, γ á gua   está o peso específico da água. Substituindo 62.4 l b / f t 3 para γ á gua   , 20 f t 2 para A , e 7.5 f t para h C G .

F   = 62.4 × 20 × 7.5   = 9360 l b f

Calcule o momento de inércia do portão retangular da seguinte forma:

I x x   = 5 × 4 3 12   = 26.66 f t 4

Passo 4

Considerando o seguinte diagrama de corpo livre para o portão

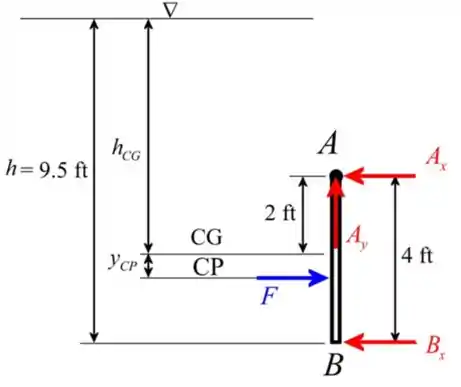
Aqui, é o centro de pressão e C P é a distância entre o centro de pressão e o centro de gravidade é y C P

Passo 5

Calcule a distância do centro de pressão e do centro de gravidade.

y C P = - I x x s i n ⁡ θ A h C G

Substitua 26.66 f t 4 por I x x , 20 f t 2 por A , 7.5 f t por h C G , e 90 ∘ p o r   θ

y C P   = - 26.66 × s i n ⁡ 90 ∘ 20 × 7.5   = - 0.178 f t

Aqui, o sinal negativo indica que o centro de pressão está abaixo do centro de gravidade.

Passo 6

(a) Calcule a força de reação horizontal em B . Considere que a soma dos momentos sobre A é zero.

  ∑   M A = 0 B x ( 4 ) - F 2 + y C P = 0

Substitua 9360 l b f para F e 0.178 f t para y C P .

B x ( 4 ) - 9360 ( 2 + 0.178 ) = 0 B x = 9360 × 2.178 4   = 5096.52 l b f

Portanto, a força de reação em B é 5096.52 l b f .

Passo 7

(b) Calcule as forças de reação da A da seguinte forma:Considere que a soma algébrica das forças na direção horizontal deve ser zero.

  ∑   F X = 0 F - B x - A x = 0 A x = F - B x

Substitua 5096.52 l b f para B x e 9360 l b f para F .

A x   = 9360 - 5096.52   = 4263.48 l b f

Considerando a soma algébrica das forças na direção vertical deve ser zero.

  ∑ y     = 0 A y = 0

Portanto, as forças de reação A nas direções horizontal e vertical são e 4263.48 l b f e 0, respectivamente.

Resposta

a) B x = 5096.52 l b f

b) A x = 4263.48 l b f e A y = 0

Exercícios de Livros Relacionados

A comporta AB tem comprimento L e largura b, está articulada em B e tem peso desprezível. O nível h do líquido permanece no topo da comporta para qualquer ângulo θ . Encontre uma expressão analítica p
A comporta B da figura abaixo tem 30 cm de altura, 60 cm de largura e é articulada no seu topo. Qual a profundidade h de água na qual terá início a abertura da comporta?
A comporta AB na figura abaixo é uma massa homogênea de 180 kg, 1,2 m de largura, é articulada em A e está apoiada sobre um fundo liso em B. Todos os fluidos estão a 20°C. Para qual profundidade h da
O tanque abaixo tem um tampão de 4 cm de diâmetro no fundo à direita. Todos os fluidos estão a 20°C. O tampão romperá se a força hidrostática sobre ele for de 25 N. Para essa condição, qual será a lei
Encontre a altura H na figura abaixo para qual a força hidrostática sobre o painel retangular é a mesma que a força sobre o painel semicircular abaixo.