Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 55
O condensador de uma planta de potência a vapor é construído com tubos de aço inoxidável AISI 302 (= 15 W/(m · K)), com diâmetros externo e interno de = 30 mm e = 26 mm, respectivamente. Vapor de água saturado a 0,135 bar condensa sobre a superfície externa de um tubo, enquanto água a uma temperatura média de = 290 K encontra-se em escoamento plenamente desenvolvido no interior do tubo.
(a) Para uma vazão de água de = 0,25 kg/s, quais são a temperatura da superfície externa do tubo e as taxas de transferência de calor e de condensação de vapor por unidade de comprimento do tubo? Como uma primeira estimativa, você pode estimar as propriedades do filme líquido na temperatura de saturação. Se alguém desejar aumentar as taxas de transferência, qual é o fator limitante que deve ser levado em conta?
(b) Explore o efeito da vazão do escoamento da água em e na taxa de transferência de calor por unidade de comprimento?
Passo 1
Tá legal! A primeira coisa que temos que fazer é ir lá no apêndice A para buscar as propriedades de interesse da água, então da tabela A.6, temos as seguintes propriedades para a temperatura média
Agora, também da tabela A.6, precisamos dos valores para o vapor saturado de água a 0,135 bar, então, teremos:
Agora, ainda da tabela A.6, precisamos pegar as propriedades na temperatura de filme, que, conforme foi dito no enunciado, pode ser aproximado pelas propriedades na temperatura de saturação, então teremos:
Então, para essa temperatura de filme, temos as seguintes propriedades para a água:
Passo 2
Então, começando de fato a letra (a) agora, podemos expressar o problema através do conceito de resistência, onde temos primeiro a resistência sendo a de filme de condensado, seguido da resistência por condução no tubo de aço e por fim a convecção com o meio externo, então, o calor por unidade de comprimento pode ser escrito em função das resistências da seguinte forma:
E, excluindo a primeira parte onde temos a resistência de contato do filme, a equação do calor por unidade de comprimento pode ser escrita como:
O que precisamos fazer então é encontrar o valor das resistências. Começando pela resistência de convecção para o escoamento interno, temos:
Para calcular esse coeficiente de convecção, vamos utilizar a correlação de Dittus-Boelter, dada por:
Para isso precisamos calcular o valor de Reynolds, que é dado por:
No entanto, temos o valor da vazão mássica, e sabemos que a sua equação é dada por:
Isolando a densidade dessa equação, chegamos em:
Passo 3
Substituindo essa expressão na equação para Reynolds, chegamos em:
E, substituindo os valores conhecidos nessa expressão, chegamos em:
E agora, substituindo os valores conhecidos na equação para o coeficiente convectivo interno, temos:
Então, a resistência de convecção será:
Passo 4
Agora vamos calcular a resistência por condução, que será dada por:
Substituindo os valores conhecidos, chegamos em:
E, agora, para a resistência de contato do filme de condensado, temos:
Então precisamos encontrar o coeficiente de convecção externo, que será dado pela equação 10.46 vista nesse capítulo, onde temos:
Então, para isso, precisamos calcular o valor do calor latente corrigido, que por sua vez é dado por:
Substituindo os valores conhecidos nessa equação, temos:
Substituindo os valores conhecidos na expressão para o coeficiente de convecção interno, chegamos em:
Então, a resistência do filme de condensado será:
Passo 5
Agora então nós vamos igualar as duas equações escritas lá no passo 2 para o calor por unidade de comprimento, de forma que chegamos em:
Substituindo os valores conhecidos, temos:
Resolvendo essa equação com o auxílio de uma calculadora, chegamos em:
E, com isso, pegando a segunda parcela dessa equação, podemos agora encontrar o calor por unidade de comprimento, de modo que teremos:
E, com isso, podemos encontrar a taxa de condensação de vapor por unidade de comprimento através de:
Passo 6
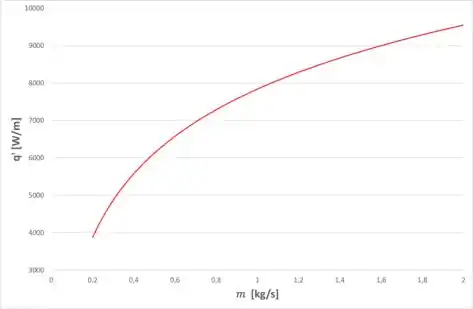
Agora, para a letra (b), precisamos estudar a influência da vazão do escoamento da água em e na taxa de transferência de calor por unidade de comprimento. Conforme vimos nos passos anteriores, foi encontrada a partir das relações de resistência, dada por:
A vazão mássica entra nessa equação através da resistência por convecção, onde temos o coeficiente de convecção interno, onde temos que calcular o número de Reynolds e nele temos a vazão mássica. Então, reescrevendo esse coeficiente lá do passo 3, só que agora deixando em função da vazão mássica, temos:
Então, a resistência a convecção será:
Então, substituindo os valores conhecidos na relação obtida a partir das resistências, temos:
Então, dessa equação conseguimos obter a seguinte relação entre a vazão mássica e a temperatura :
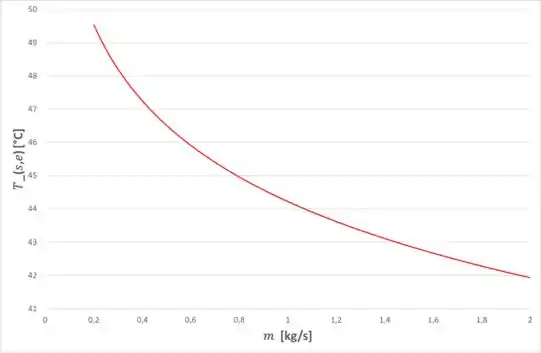
Passo 7
Agora, para obter uma relação entre a vazão mássica e o calor por unidade de comprimento, basta utilizar a relação anterior e alguma parcela da equação de resistência escrita anteriormente, igual fizemos no passo 5, então, com isso, teremos o seguinte gráfico:
