Para as condições do Problema 4.48, estime o tempo requerido para drenar o tanque à profundidade de (uma mudança na profundidade de ), e de para (também uma mudança na profundidade de ). Você pode explicar a discrepância nesses tempos? Trace o gráfico do tempo de drenagem do tanque como função do diâmetro do furo na profundidade do tanque variando de para .

Feito as considerações, podemos usar e equação da conservação de massa para o volume de controle.

A equação básica se torna

Podemos aqui, fazer as seguintes substituições:

e

Substituindo na equação encontrada no passo 2 temos:

Podemos agora integrar dos dois lados.

Podemos encontrar a função , que determina a profundidade no tanque, substituindo os valores fornecido no enunciado na equação encontrada no passo anterior. Assim temos:

Para calcular os tempos requerido para drenar o tanque, basta usamos a função que encontramos no passo anterior.

Para a profundidade de a :

Portanto, o tempo de drenagem quando é

Para a profundidade de a :

Quando a profundidade  e o tempo gasto são milissegundos e quando a profundidade  o tempo gasto é milissegundos.

A mudança de tempo durante a mudança de profundidade 1 pé é

Portanto, o tempo de drenagem de para é .

Assim, à medida que a profundidade diminui, o tempo necessário para a taxa de drenagem aumenta.

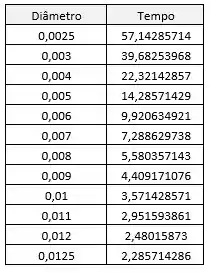
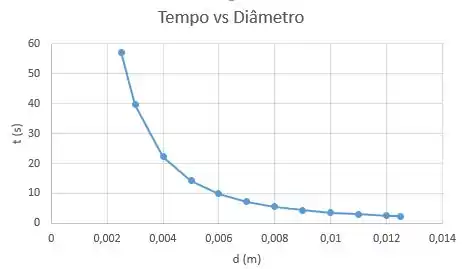
Podemos usar a seguinte equação para traçar o gráfico do tempo de drenagem do tanque como função do diâmetro do furo na profundidade do tanque variando de para .

Para isso substituímos os valores da seguinte maneira:

Aqui, temos a tabela e o gráfico tempo em função do diâmetro usando o software Microsoft Excel. Usando a equação acima variando o diâmetro do furo no tanque, temos a seguinte tabela: