Um funil cônico, com meio ângulo , com diâmetro máximo e altura , deixa escapar líquido por um orifício (diâmetro ) no seu vértice. A velocidade do líquido deixando o reservatório é dada, aproximadamente, por em que é a altura da superfície livre do líquido acima do orifício. Determine a taxa de variação do nível da superfície no reservatório no instante em que .

Podemos fazer um esboço do volume de controle da seguinte maneira

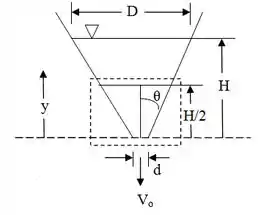
Onde o volume de controle é referido como o tracejado pontilhado.

Podemos aplicar a equação da continuidade no volume de controle desenhado. Assim temos:

Pelas considerações feitas:

Podemos rescrever a equação encontrada no passo anterior sabendo que:

Pois está diminuindo.

Podemos dizer também que:

e

Pois

Podemos também escrever como:

E como foi dito no enunciado:

Substituindo na equação temos:

Para calcular a taxa de variação do nível da superfície no reservatório no instante em que , bata substituirmos os valores fornecido no enunciado na equação encontrada no passo anterior.