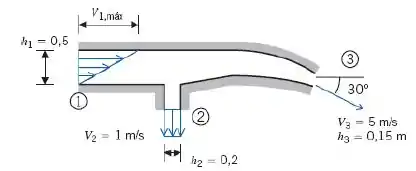
Uma curva redutora bidimensional tem um perfil de velocidade linear na seção . O escoamento é uniforme nas seções e . O fluido é incompressível e o escoamento é permanente. Determine o módulo e o sentido da velocidade uniforme na seção .

Na seção 1, a velocidade é  e a área da superfície de controle é . Podemos escrever o perfil de velocidade na seção 1 como:

Pois, podemos perceber que a velocidade fica é máxima quando e decresce linearmente até quando .

Podemos escrever como função de apenas uma componente, pois só há variação em . Assim podemos considerar a profundidade como um valor , e escrever o diferencial de área como:

Na seção 2 e 3 foi dito que o escoamento é uniforme, logo, as velocidades são constantes e foram dadas no enunciado. Assim como na seção 1, na seção 2 e 3 o diferencial de área pode ser escrito como:

Podemos então aplicar a equação da continuidade:

Substituindo os termos, temos:

Precisamos agora examinar as direções dos vetores. Na seção 1 o vetor de área e velocidade agem em sentidos opostos, logo, o resultado do produto escalar é negativo. Na seção 2 e 3 o vetor velocidade a área agem no mesmo sentido, logo, o produto escalar é positivo. Portanto:

Agora, podemos resolver a equação resolvendo as integrais. Na seção 1 o limite de integração é de a , na seção 2 o limite de integração é de a e na seção 3 o limite de integração é de a . Assim temos:

Para encontrarmos o valor de , basta substituirmos os valores dados no enunciados para cada componente da equação encontrada acima. Substitua por , por , por , por  e por .

Portanto, a velocidade máxima na seção 1 é .