Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 77
Um tanque com diâmetro inicialmente está cheio com água até acima do centro de uma válvula com diâmetro próxima à parte inferior. A superfície do tanque está aberta para a atmosfera e o tanque é drenado por meio de um tubo com comprimento de conectado à válvula. O fator de atrito do tubo é dado por e a velocidade de descarga é expressa por , onde é a altura da água acima do centro da válvula. Determine (a) a velocidade inicial de descarga do tanque e (b) o tempo necessário para esvaziar o tanque. O tanque pode ser considerado vazio quando o nível da água cai até o centro da válvula.
Passo 1
vamos fazer uma ilustração do nosso tanque, simples, mas é suficiente vai.
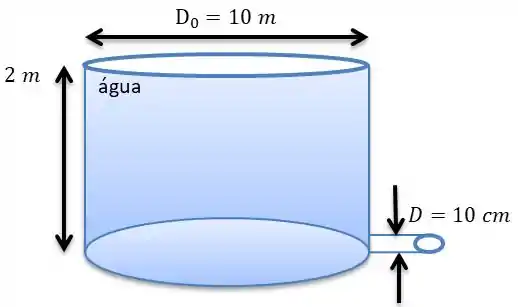
Vamos assumir que o fluxo é constante e iramos considerar que o tanque estará vazio quando o nível da água chegar até centro da válvula.
Passo 2
a) Para calculara a velocidade inicial da água, basta substituirmos os valores que foi nos dado no enunciado na formula que também foi dado:
Só vamos ficar atentos que desejamos a velocidade inicial, portanto, utilizaremos a coluna de água inicial, ou seja, tanque cheio .
Passo 3
b) Para determinar a quantidade de tempo para esvaziar o tanque, primeiramente temos que determinar a vazão volumétrica:
Substituindo os valores que são constantes durante o processo:
Não irei finalizar possíveis, para facilitar à escrita. Apenas uma questão de jogar na calculadora.
Passo 4
Perceba que é a nossa variável que estará variando com o tempo, portanto caso nós desejamos descobrir a quantidade de água que flui pelo duto durante o processo, vamos diferenciar o fluxo, nossa notação para volume será devido termo vários nos nossos calculos:
E como nós assumimos que o fluxo é constante e incompressível, temos que pela conservação da massa, a quantidade de água que passa pelo duto vai ser igual à quantidade de água que tem no tanque.
Em que é variação do nível de água do tanque um período de tempo . Note que coloquei , pois a direção positiva de é para cima, com estamos esvaziando o tanque a varia de será negativa.
Igualando as duas equações:
Isolando , pois é a grandeza tempo que desejamos, para esta certa quantidade de água:
Passo 5
Determinamos a equação do tempo para esvaziar esta variação de volume, agora é uma questão de calculo apenas, como sabemos a integral de uma derivada é a variável que esta sendo diferenciada, portanto integrando dos dois lados da equação:
Note que, não podemos simplesmente integrar, pois temos limites para esta integral, limites físicos. Em que para , significa que nosso tanque começou a esvaziar, portanto, para a correspondente de , no espaço físico, e para o tempo necessário para esvaziar teremos seu correspondente espaço .
Simplificando a integral:
Substituindo e executando os cálculos, temos:
Para termos uma noção melhor do que significa isso, dividindo por 60:
Dividindo novamente por 60: