Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 4.Problemas - Ex. 59

Considere uma aleta plana triangular, bidimensional, com comprimento L = 50   m m e espessura na base de t = 20   m m . A condutividade térmica da aleta é k = 25   W / m · K . A temperatura de sua base é T b = 50 ° C e a aleta está exposta a condições convectivas caracterizadas por h = 50   W / m 2 · K e T ∞ = 20 ° C . Usando uma malha de diferenças finitas com Δ x = 10   m m e Δ y = 2   m m , e aproveitando a simetria, determine a eficiência de aleta, η a . Compare o seu valor para a eficiência da aleta com o informado na Figura 3.19.

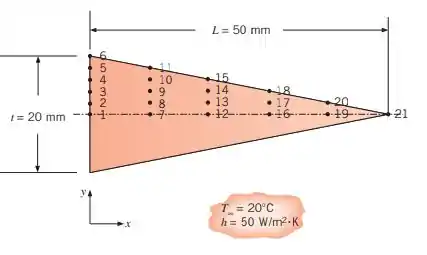
Passo 1

Começamos o nosso problema calculando um ∆ l , que será a hipotenusa dos nossos triângulos menores dentro do nosso triângulo:

∆ l 2 = ∆ x 2 + ∆ y 2

∆ l = 10 2 + 2 2

∆ l = 10,2   m m

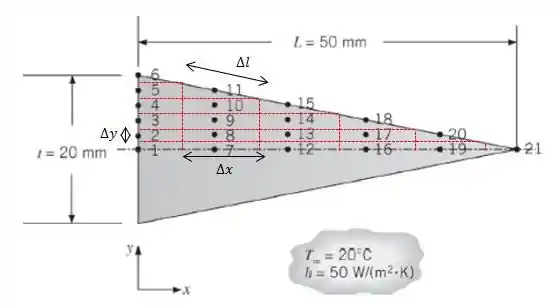
A eficiência da aleta é dada pela seguinte equação:

n a = q a ' h A a θ b

Com:

h = 50   W / m 2 ⋅ K

θ b = T b - T ∞ = 50 - 20 = 30 ° C

Devemos calcular a área da aleta triangular:

A a = 2 L 2 + t 2 2

A a = 2 0,05 2 + 0,02 2 2

A a = 0,102   m

Podemos utilizar a seguinte equação para obtermos o calor:

q a ' = 2 k ∆ y ∆ x T 1 - T 7 2 + T 2 - T 8 + T 3 - T 9 + T 4 - T 10 + T 5 - T 11 2

q a ' = 2 ⋅ 25 ⋅ 2 10 ⋅ T 1 - T 7 2 + T 2 - T 8 + T 3 - T 9 + T 4 - T 10 + T 5 - T 11 2

q a ' = 5 ⋅ T 1 - T 7 + 2 ⋅ T 2 - T 8 + 2 ⋅ T 3 - T 9 + 2 ⋅ T 4 - T 10 + T 5 - T 11

Pela figura, percebemos que:

T 1 = T 2 = T 3 = T 4 = T 5 = T 6 = 50 ° C

Assim:

q a ' = 5 ⋅ - T 7 - 2 T 8 - 2 T 9 - 2 T 10 - T 11 + 400

Passo 2

Os nós no interior são calculados usado a fórmula:

T i = 1 4 ∑ T v i z

Bora calcular!

4 T 7 = T 1 + 2 T 8 + T 12

4 T 8 = T 2 + T 7 + T 13 + T 9

4 T 9 = T 3 + T 8 + T 14 + T 10

4 T 10 = T 4 + T 9 + T 15 + T 11

4 T 12 = T 6 + 2 T 13 + T 16

4 T 13 = T 8 + T 12 + T 17 + T 14

4 T 14 = T 9 + T 13 + T 18 + T 15

4 T 16 = T 12 + 2 T 17 + T 19

4 T 17 = T 13 + T 16 + T 20 + T 18

4 T 19 = T 16 + 2 T 20 + T 21

No Ponto 11:

h ∆ l k + 2 T 11 = T 5 + T 10 + h ∆ l k T ∞

Calculando h ∆ l k :

h ∆ l k = 50 ⋅ 0 , 00102 25 = 0,02

Então:

2,02 T 11 = T 5

No Ponto 15:

2,02 T 15 = T 10 + T 14 + 0,4

Na Ponto 18:

2,02 T 18 = T 14 + T 17 + 0,4

No Ponto 20:

2,02 T 20 = T 17 + T 19 + 0,4

No Ponto 21:

h ∆ l k + 1 T 2 1 = T 1 9 + h ∆ l k T ∞

Então:

1,02 T 21 = T 19 + 0,4

Calculando as temperaturas com um programa matemático:

T 7 = T 8 = T 9 = T 10 = T 11 = 47,6 ° C

T 12 = T 13 = T 14 = T 15 = 45,3 ° C

T 16 = T 17 = T 18 = 43,11 ° C

T 19 = T 20 = 41,03 ° C

T 21 = 39,09 ° C

Passo 3

Agora, podemos calcular o nosso calor:

q a ' = 5 ⋅ - T 7 - 2 T 8 - 2 T 9 - 2 T 10 - T 11 + 400

q a ' = 5 ⋅ - 47,6 - 2 ⋅ 47,6 - 2 ⋅ 47,6 - 2 ⋅ 47,6 - 47,6 + 400

q a ' = 109   W / m

Com o calor, encontramos a nossa eficiência:

n a = q a ' h A a θ b

n a = 109 50 ⋅ 0,102 ⋅ 30

n a = 0,71

Passo 4

Pela Figura 3.19, temos:

L c 3 2 h k A p 1 2 = L c 3 2 2 h k L t 1 2 = 0,05 3 2 ⋅ 2 ⋅ 50 25 ⋅ 0,05 ⋅ 0,02 1 2

L c 3 2 h k A p 1 2 = 0,707

Observando a figura, obtemos:

n a = 0,78

Assim, obtemos valores próximos!

Resposta

n a = 0,71

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr
Uma parede plana ( ρ=4000k g / m 3,c p=500J / ( k g·K ) ,k=10W / ( m·K ) ) , com espessura L=20m m , tem inicialmente uma distribuição de temperaturas estacionária linear, com as superfícies mantidas
A superfície superior de uma placa, incluindo os seus sulcos, é mantida a uma temperatura uniforme T 1=200 ° C . A superfície inferior se encontra a T 2=20 ° C . A condutividade térmica da placa é de