Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 112
Uma parede plana com espessura , tem inicialmente uma distribuição de temperaturas estacionária linear, com as superfícies mantidas a e . Subitamente, uma corrente elétrica é passada através da parede, causando geração de energia uniforme a uma taxa . As condições de contorno e permanecem fixas.
(a) Em coordenadas , esboce distribuições de temperaturas para os seguintes casos: (i) condição inicial (ii) condição de regime estacionário supondo que a temperatura máxima na parede é superior a e (iii) para dois tempos intermediários. Identifique todas as principais características das distribuições.
(b) Para o sistema com três pontos nodais mostrado na figura defina um volume de controle apropriado para o nó m e, identificando todos os processos relevantes, deduza a equação de diferenças finitas correspondente usando o método explícito ou o método implícito.
(c) Com um incremento de tempo , use o método de diferenças finitas para obter valores de para os primeiros . Determine os fluxos térmicos correspondentes nos dois contornos, isto é, e
(d) Para determinar o efeito do tamanho da malha, repita a sua análise usando malhas com 5 e 11 pontos nodais ( e , respectivamente).
Passo 1
Aqui nós temos uma parede plana, inicialmente com uma distribuição linear de temperatura em estado estacionário com limites mantidos em e , experimentando uma geração de calor volumétrica uniforme devido à corrente elétrica. Onde as condições de contorno e permanecem fixadas com o tempo.
A partir dessas informações nós queremos esboçar as distribuições de temperatura para diferentes casos, derivar a equação da diferença finita usando o método implícito ou explícito, obter valores de para os primeiros do tempo decorrido e determinar os fluxos de calor correspondentes nos limites.
E por último, determinar o efeito do tamanho da malha repetindo a análise anterior usando grades de e pontos nodais. Eu sei que parece muito mas juntinhos a gente consegue, beleza?
Passo 2
Para resolver essa questão vamos assumir que a condução é transitória e bidimensional, a geração de calor volumétrico é uniforme para e as propriedades são constantes.
Na letra (a) queremos, em coordenadas , esboçar as distribuições de temperaturas para alguns casos. A distribuição de temperatura nas coordenadas T-x para os casos solicitados é mostrada abaixo.
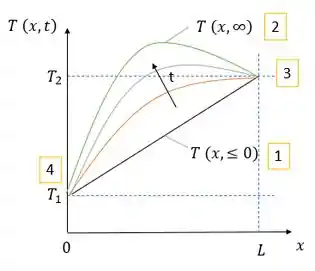
Onde,
(1) Distribuição linear inicial de temperatura
(2) Distribuição de temperatura no estado estacionário parabólico não simétrico
(3) O gradiente em é o primeiro positivo, depois zero e torna-se negativo
(4) O gradiente em é sempre positivo.
Passo 3
Na letra (b) queremos deduzir a equação de diferenças finitas. Fazendo um balanço de energia no volume de controle sobre o nó , para a área da unidade, chegamos em:
Inserindo o número de Fourier:
Para o termo entre parênteses, usamos "p" para explícito e "p + 1" para forma implícito,
Explícito:
Implícito:
Passo 4
Na letra (c) nós queremos os fluxos térmicos correspondentes nos dois contornos. Com um incremento de tempo , as equações anteriores passam a ser:
Explícito:
Implícito:
Onde,
Realizando os cálculos, os resultados são tabulados em função do tempo:
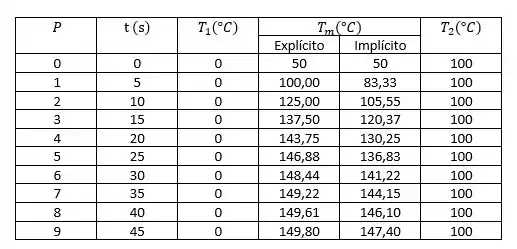
Passo 5
O fluxo de calor nos limites em segue dos balanços de energia nos volumes de controle sobre os nós dos limites, usando os resultados explícitos para
Nó 1:
Nó 2:
Passo 6
Na letra (d) nós queremos repetir a análise anterior usando malhas com 5 e 11 pontos nodais, e respectivamente. Os resultados são tabulados abaixo para , em que é o nó central.
Resposta
(a)
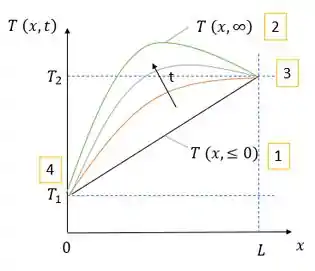
(b) Explícito:
Implícito:
(c) e
(d)
