Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e em uma de suas extremidades. No tempo t=0 , calor é aplicado na extremidade restante do cilindro, causando um aumento linear de T 0 com o tempo a uma taxa de 1 ° C / s .(a) Usando o método explícito com F o=½ , ½ deduza as equações de diferenças finitas para os nós 1 ,2 ,3 e 4 . (b) Faça uma tabela que apresente as seguintes colunas: p ,t ( s ) e as temperaturas nodais de T 0 a T 4 . Determine a temperatura na superfície T 0 quando T 4=35 ° C .

m= 1,2 , 3 e 4 T m p + 1 = F o T m + 1 p + T m - 1 p + 1 - 2 F o T m p = 0,5 T m + 1 p + T m - 1 p m= 4 T 4 p + 1 = 2 F oT 3 p + 1 - 2 F o T 4 p = T 3 p Quando T 4( 210 s ,p=7 )=35°C , encontramos queT 0( 210 s )=230°C .

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 113

Um cilindro sólido redondo, feito com um material plástico está inicialmente a uma temperatura uniforme de e se encontra isolado ao longo de sua superfície lateral e em uma de suas extremidades. No tempo , calor é aplicado na extremidade restante do cilindro, causando um aumento linear de com o tempo a uma taxa de .

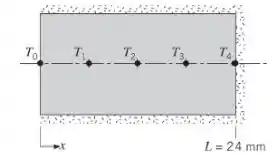
(a) Usando o método explícito com deduza as equações de diferenças finitas para os nós e .

(b) Faça uma tabela que apresente as seguintes colunas: e as temperaturas nodais de a . Determine a temperatura na superfície quando .

Passo 1

Oiee, vamos para mais uma questão? 😊. Aqui nós temos um cilindro sólido de material plástico inicialmente em temperatura uniforme de , isolada em uma extremidade ), enquanto outra extremidade experimenta aquecimento, fazendo com que sua temperatura aumente linearmente com o tempo a uma taxa de .

Com essas informações, queremos encontrar as equações de diferenças finitas para os nós usando o método explícito com e a temperatura da superfície quando . Então vamos lá!

Passo 2

Para resolver essa questão vamos assumir que a condução transitória é unidimensional no cilindro, as propriedades são constantes e as superfícies laterais e finais são perfeitamente isoladas.

As equações de diferença finita usando o método explícito para os nós interiores com são:

A partir de um balanço de energia no nó de volume de controle com , temos:

Passo 3

Fazendo os cálculos, o histórico de temperatura-tempo é tabulado abaixo, onde , e com,

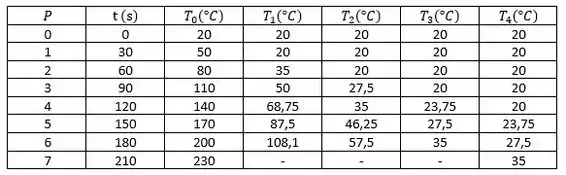
Quando , encontramos que.

Resposta

m= e

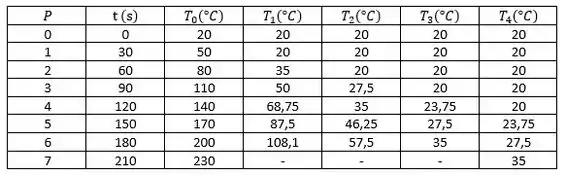
Quando , encontramos que.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a malha bidimensional ( ∆ x = ∆ y ) representando condições de regime estacionário, sem geração volumétrica interna de calor, em um sistema com condutividade térmica k . Um dos contornos é mantid

Determine as expressões para q ( m - 1 , n ) → ( m , n ) ,q m + 1 , n → ( m , n ) ,q m ,n + 1 → ( m , n ) e q m ,n - 1 → ( m , n ) , na condução associada a um volume de controle que abrange dois dife

Deduza as equações de diferenças finitas nodais para as seguintes considerações.(a) Nó (m,n) sobre um contorno diagonal sujeito à convecção com um fluido a uma temperatura T ∞ , com um coeficiente de

Seja uma aleta unidimensional, com área de seção transversal uniforme, isolada na sua extremidade, x = L . A temperatura na base da aleta T b e a do fluido vizinho T ∞ , bem como o coeficiente de tran

Considere a rede para um sistema bidimensional, sem geração volumétrica interna de calor, que tem as temperaturas nodais mostradas a seguir. Sendo o espaçamento da malha de 125m m e a condutividade té