Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 74

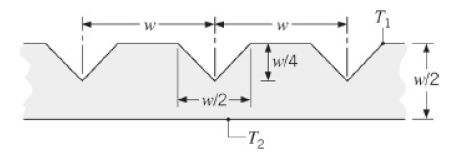
A superfície superior de uma placa, incluindo os seus sulcos, é mantida a uma temperatura uniforme T 1   =   200 ° C . A superfície inferior se encontra a T 2   =   20 ° C . A condutividade térmica da placa é de 15 W m K e o espaçamento entre os sulcos é de   0,16   m .

  1. Usando um método de diferenças finitas com um tamanho de malha de Δ x   =   Δ y   =   40   m m , calcule as temperaturas nodais desconhecidas e a taxa de transferência de calor por largura do espaçamento dos sulcos (w) e por unidade de comprimento normal à página.
  2. Com um tamanho de malha de Δ x   =   Δ y   =   10   m m , repita os cálculos anteriores, determinando o campo de temperaturas e a taxa de transferência de calor. Analise, também, condições nas quais a superfície inferior não se encontra a uma temperatura uniforme T 2 , mas está exposta a um fluido com T ∞   =   20 ° C . Com Δ x   =   Δ y   =   10   m m , determine o campo de temperaturas e a taxa de transferência de calor para valores de h   =   5 ,   200 e 1000 W m 2 K , bem como para h   →   ∞ .

Passo 1

Boom galerinha, vamos começar?

Vamos começar desenhando o que está acontecendo neste problema, na letra (a) nós vamos fazer Δ x   =   Δ y   =   40   m m   e dois eixos de simetria adiabática, uma no sulco e outra na metade do caminho de um sulco ao outro:

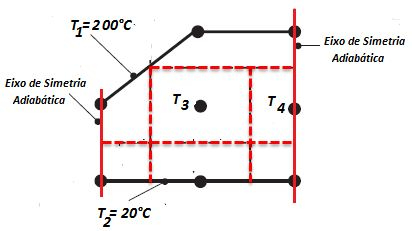
No desenho fica mais fácil de achar as outras duas temperaturas que ainda não temos, T 3   e T 4 :

Como os dois nós são internos, para o Ponto 3:

4 T 3 = 2 T 1 + T 2 + T 4

Substituindo as temperaturas que nos foi dada:

4 T 3 = 4 20 + T 4     →     T 4 = 4 T 3 - 420

Ponto 4:

4 T 4 = T 1 + T 2 + 2 T 3

4 T 4 = 220 + 2 T 3

Substituindo T 4 :

4 4 T 3 - 220 = 220 + 2 T 3

T 3 = 135,7 ° C

E achando T 4 :

4 T 4 = 220 + 2 135,7 ° C

T 4 = 122,9 ° C

E para finalizar a letra a nós precisamos da taxa de transferência de calor, certo?

Nós temos aqui três pontos, T 1 ,   T 3 e T 4 transferindo calor por condução para o ponto T 2 :

q ' = q ' 1 + q ' 3 + q ' 4

q ' = k ∆ x 2 T 1 -   T 2 ∆ y + k ∆ x T 3 -   T 2 d y + k ∆ x 2 T 4 -   T 2 ∆ y

Como ∆ x = ∆ y :

q ' = 15 W m K 200 ° C -   20 ° C 2 + 135,7 ° C -   20 ° C + 122,9 ° C -   20 ° C 2

q ' = 3,86 k W m

Como nós temos duas partes iguais entre os sulcos:

q ' t o t a l = 2 × 3,86 k W m = 7,72 k W m

Passo 2

Na letra (b) nós devemos fazer Δ x   =   Δ y   =   10   m m :

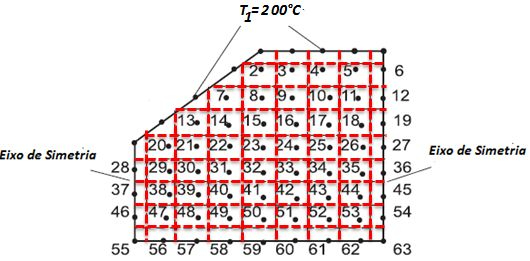
Como os pontos de 2 até 54 são internos:

4 T 2 = 2 T 1 + T 3 + T 8

4 T 3 = T 1 + T 2 + T 4 + T 9

4 T 4 = T 2 + T 3 + T 5 + T 10

4 T 5 = T 3 + T 4 + T 6 + T 11

4 T 6 = T 4 + 2 T 5 + T 12

4 T 7 = 2 T 1 + T 8 + T 1 4

4 T 8 = T 2 + T 7 + T 9 + T 15

4 T 9 = T 3 + T 8 + T 10 + T 16

4 T 10 = T 4 + T 9 + T 11 + T 17

4 T 11 = T 5 + T 10 + T 12 + T 18

4 T 12 = T 6 + 2 T 11 + T 19

4 T 13 = 2 T 1 + T 14 + T 21

4 T 14 = T 7 + T 13 + T 15 + T 22

4 T 15 = T 8 + T 14 + T 16 + T 23

4 T 16 = T 9 + T 15 + T 17 + T 24

4 T 17 = T 10 + T 16 + T 18 + T 25

4 T 18 = T 11 + T 17 + T 19 + T 26

4 T 19 = T 12 + 2 T 18 + T 27

4 T 20 = 2 T 1 + T 21 + T 29

4 T 21 = T 13 + T 20 + T 22 + T 30

4 T 22 = T 14 + T 21 + T 23 + T 31

4 T 23 = T 15 + T 22 + T 24 + T 32

4 T 24 = T 16 + T 23 + T 25 + T 33

4 T 25 = T 17 + T 24 + T 26 + T 34

4 T 26 = T 18 + T 25 + T 27 + T 35

4 T 27 = T 19 + 2 T 26 + T 36

4 T 28 = T 1 + 2 T 29 + T 37

4 T 29 = T 20 + T 28 + T 30 + T 38

4 T 30 = T 21 + T 29 + T 31 + T 39

4 T 31 = T 22 + T 30 + T 32 + T 40

4 T 32 = T 23 + T 31 + T 33 + T 41

4 T 33 = T 24 + T 32 + T 34 + T 42

4 T 3 4 = T 2 5 + T 3 3 + T 3 5 + T 4 3

4 T 35 = T 26 + T 34 + T 36 + T 44

4 T 36 = T 27 + 2 T 35 + T 45

4 T 37 = T 28 + 2 T 38 + T 46

4 T 38 = T 29 + T 37 + T 39 + T 47

4 T 39 = T 30 + T 38 + T 40 + T 48

4 T 40 = T 31 + T 39 + T 41 + T 49

4 T 41 = T 32 + T 40 + T 42 + T 50

4 T 42 = T 33 + T 41 + T 43 + T 51

4 T 43 = T 34 + T 42 + T 44 + T 52

4 T 44 = T 35 + T 43 + T 45 + T 53

4 T 45 = T 36 + 2 T 44 + T 54

4 T 46 = T 37 + 2 T 47 + T 55

4 T 47 = T 38 + T 46 + T 48 + T 56

4 T 48 = T 39 + T 47 + T 49 + T 57

4 T 49 = T 40 + T 48 + T 50 + T 58

4 T 50 = T 41 + T 49 + T 51 + T 59

4 T 51 = T 42 + T 50 + T 51 + T 60

4 T 52 = T 43 + T 51 + T 52 + T 61

4 T 53 = T 44 + T 52 + T 53 + T 62

4 T 54 = T 45 + 2 T 53 + T 63

Os demais pontos estão em uma superfície plana com convecção:

2 h ∆ x k - 2 T 55 = 2 T 4 6 + 2 T 5 6 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 5 6 = 2 T 4 7 + T 5 5 + T 5 7 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 5 7 = 2 T 4 8 + T 5 6 + T 5 8 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 5 8 = 2 T 49 + T 5 7 + T 5 9 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 5 9 = 2 T 50 + T 5 8 + T 60 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 60 = 2 T 5 1 + T 5 9 + T 6 1 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 61 = 2 T 5 2 + T 60 + T 6 2 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 62 = 2 T 5 3 + T 61 + T 6 3 + 2 h ∆ x k   T ∞

2 h ∆ x k - 2 T 63 = 2 T 5 4 + 2 T 62 + 2 h ∆ x k   T ∞

Agora nós vamos lançar todos estes dados no software IHT, como a letra (b) pediu para analisarmos o coeficiente convectivo tendendo ao infinito, como h = 10 7 W m 2 K , nossas temperaturas ficarão assim:

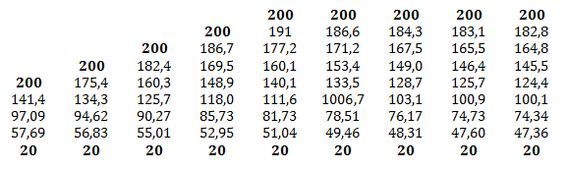
Quando comparamos com a letra (a) percebemos que aqui T 3 ,   a vai equivaler ao T 23 = 140,1 ° C ,   enquanto T 4 ,   a vai equivaler ao T 2 7 = 124,4 ° C .

Bem próximos, certo? Portanto, quanto maior o coeficiente convectivo, mais o resultado entre as duas malhas de aproxima!!

Passo 3

Agora nós vamos calcular a taxa de transferência de calor para este segundo caso!!

Seguindo a mesma lógica do passo 1:

q ' t o t a l = 2 k T 46 -   T 55 2 + T 4 8 -   T 5 7 + T 4 9 -   T 5 8 + T 50 -   T 5 9 + T 51 -   T 60 + T 52 -   T 61 + T 53 -   T 62 + T 54 -   T 63 2

Substituindo as temperatura do Passo 2:

q ' t o t a l = 7,61 k W m

E ficamos por aqui galerinhaa !!

Resposta

  1. T 3 = 135,7 ° C         T 4 = 122,9 ° C       q ' t o t a l = 7,72 k W m ;
  2. T 3 = 140,1 ° C         T 4 = 124,4 ° C       q ' t o t a l = 7 , 61 k W m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Temperaturas em regime estacionário em pontos nodais escolhidos da seção simétrica de um canal de escoamento são conhecidas: T 2 = 95,47 ° C , T 3 = 117,3 ° C , T 5 =79,79 ° C , T 6 =77,29 ° C , T 8 =
Seja um dissipador de calor de alumínio k=240 W m K , como o mostrado esquematicamente no Problema 4.28. As larguras interna e externa do canal quadrado são w = 20 mm e W = 40 mm, respectivamente, e u
A condução no interior de geometrias relativamente complexas pode, às vezes, ser avaliada usando métodos de diferenças finitas deste livro, que podem ser aplicados em subdomínios e depois unidos. Cons
As temperaturas (°C), em regime estacionário, associadas a pontos nodais selecionados em um sistema bidimensional com uma condutividade térmica de 1,5 W m K , são mostradas na malha mostrada na figura
Seja uma longa barra com seção transversal quadrada (0,8 m de lado) e condutividade térmica de 2 W m K . Três laterais da barra são mantidas a uma temperatura uniforme de 300°C. A quarta superfície es